|
|
|
The radius of a Triangle's Incircle or of a Polyhedron's Insphere, denoted ![]() . For a
Triangle,
. For a
Triangle,
 |
(1) | ||
| (2) |
Equation (1) can be derived easily using Trilinear Coordinates. Since the Incenter is equally spaced from all
three sides, its trilinear coordinates are 1:1:1, and its exact trilinear coordinates are ![]() . The ratio
. The ratio ![]() of the exact
trilinears to the homogeneous coordinates is given by
of the exact
trilinears to the homogeneous coordinates is given by
| (3) |
| (4) |
Other equations involving the inradius include
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
As shown in Right Triangle, the inradius of a Right Triangle of integral side lengths ![]() ,
, ![]() , and
, and ![]() is also
integral, and is given by
is also
integral, and is given by
| (10) |
| (11) |
| (12) |
Expressing the Midradius ![]() and Circumradius
and Circumradius ![]() in terms of the midradius gives
in terms of the midradius gives
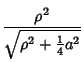 |
(13) | ||
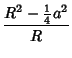 |
(14) |
See also Carnot's Theorem, Circumradius, Midradius
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, 1929.
Mackay, J. S. ``Historical Notes on a Geometrical Theorem and its Developments [18th Century].''
Proc. Edinburgh Math. Soc. 5, 62-78, 1886-1887.
Mackay, J. S. ``Formulas Connected with the Radii of the Incircle and Excircles of a Triangle.''
Proc. Edinburgh Math. Soc. 12, 86-105.
Mackay, J. S. ``Formulas Connected with the Radii of the Incircle and Excircles of a Triangle.''
Proc. Edinburgh Math. Soc. 13, 103-104.
|
|
|
© 1996-9 Eric W. Weisstein