|
|
|
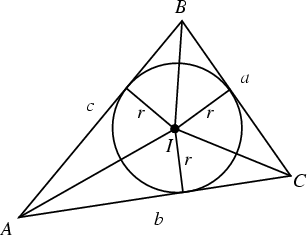
The Inscribed Circle of a Triangle ![]() . The center
. The center ![]() is called the Incenter and the
Radius
is called the Incenter and the
Radius ![]() the Inradius. The points of intersection of the incircle with
the Inradius. The points of intersection of the incircle with ![]() are the Vertices of the Pedal Triangle of
are the Vertices of the Pedal Triangle of ![]() with the Incenter as the Pedal Point (c.f. Tangential
Triangle). This Triangle is called the Contact Triangle.
with the Incenter as the Pedal Point (c.f. Tangential
Triangle). This Triangle is called the Contact Triangle.
The Area ![]() of the Triangle
of the Triangle ![]() is given by
is given by
Using the incircle of a Triangle as the Inversion Center, the sides of the Triangle and its Circumcircle are carried into four equal Circles (Honsberger 1976, p. 21). Pedoe (1995, p. xiv) gives a Geometric Construction for the incircle.
See also Circumcircle, Congruent Incircles Point, Contact Triangle, Inradius, Triangle Transformation Principle
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 11-13,
1967.
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., 1976.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, pp. 182-194, 1929.
Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., 1995.