|
|
|
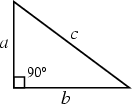
A Triangle with an Angle of 90° (![]() radians). The sides
radians). The sides ![]() ,
, ![]() , and
, and ![]() of such a Triangle
satisfy the Pythagorean Theorem. The largest side is conventionally denoted
of such a Triangle
satisfy the Pythagorean Theorem. The largest side is conventionally denoted ![]() and is called the
Hypotenuse.
and is called the
Hypotenuse.
For any three similar shapes on the sides of a right triangle,
| (1) |
| (2) |
| (3) |
| (4) | |||
| (5) | |||
| (6) |
| (7) |

Given a right triangle ![]() , draw the Altitude
, draw the Altitude ![]() from the Right Angle
from the Right Angle ![]() . Then the
triangles
. Then the
triangles ![]() and
and ![]() are similar.
are similar.
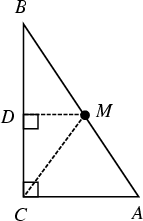
In a right triangle, the Midpoint of the Hypotenuse is equidistant from the three Vertices (Dunham 1990). This can be proved as follows. Given ![]() , let
, let ![]() be the Midpoint of
be the Midpoint of ![]() (so that
(so that
![]() ). Draw
). Draw ![]() , then since
, then since ![]() is similar to
is similar to ![]() , it follows that
, it follows that ![]() . Since both
. Since both ![]() and
and ![]() are right triangles and the corresponding legs are equal, the Hypotenuses are also
equal, so we have
are right triangles and the corresponding legs are equal, the Hypotenuses are also
equal, so we have ![]() and the theorem is proved.
and the theorem is proved.
See also Acute Triangle, Archimedes' Midpoint Theorem, Brocard Midpoint, Circle-Point Midpoint Theorem, Fermat's Right Triangle Theorem, Isosceles Triangle, Malfatti's Right Triangle Problem, Obtuse Triangle, Pythagorean Triple, Quadrilateral, RAT-Free Set, Triangle
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 121, 1987.
Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 120-121, 1990.
|
|
|
© 1996-9 Eric W. Weisstein