Isosceles Triangle

A Triangle with two equal sides (and two equal Angles). The name derives from the Greek iso (same) and skelos (Leg). The height of the above isosceles triangle can be found from the Pythagorean Theorem as

$$h=\sqrt{b^2-{\textstyle{1\over 4}}a^2}.$$ (1)

The Area is therefore given by

$$A={\textstyle{1\over 2}}ah={\textstyle{1\over 2}}a\sqrt{b^2-{\textstyle{1\over 4}}a^2}.$$ (2)

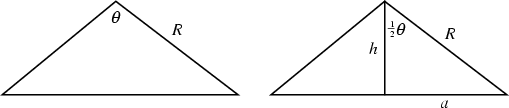
There is a surprisingly simple relationship between the Area and Vertex Angle $\theta$. As shown in the above diagram, simple Trigonometry gives

$$h = R\cos({\textstyle{1\over 2}}\theta)$$ (3)

$$a = R\sin({\textstyle{1\over 2}}\theta),$$ (4)

so the Area is

$$A={\textstyle{1\over 2}}(2a)h=ah=R^2\cos({\textstyle{1\over ... ...xtstyle{1\over 2}}\theta)={\textstyle{1\over 2}}R^2\sin\theta.$$ (5)

No set of $n>6$ points in the Plane can determine only Isosceles Triangles.

See also Acute Triangle, Equilateral Triangle, Internal Bisectors Problem, Isosceles Tetrahedron, Isoscelizer, Obtuse Triangle, Point Picking, Pons Asinorum, Right Triangle, Scalene Triangle, Steiner-Lehmus Theorem