|
|
|

An equilateral triangle is a Triangle with all three sides of equal length ![]() . An equilateral triangle also has
three equal 60° Angles.
. An equilateral triangle also has
three equal 60° Angles.
An equilateral triangle can be constructed by Trisecting all three Angles of any Triangle (Morley's Theorem). Napoleon's Theorem states that if three equilateral triangles are drawn on the Legs of any Triangle (either all drawn inwards or outwards) and the centers of these triangles are connected, the result is another equilateral triangle.
Given the distances of a point from the three corners of an equilateral triangle, ![]() ,
, ![]() , and
, and ![]() , the length of a side
, the length of a side
![]() is given by
is given by
| (1) |
The Altitude ![]() of an equilateral triangle is
of an equilateral triangle is
| (2) |
| (3) |
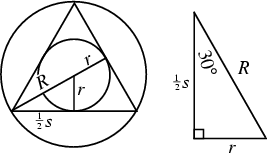
The Inradius ![]() , Circumradius
, Circumradius ![]() , and Area
, and Area ![]() can be computed directly from the formulas for a
general regular Polygon with side length
can be computed directly from the formulas for a
general regular Polygon with side length ![]() and
and ![]() sides,
sides,
| (4) | |||
| (5) | |||
| (6) |
| (7) | |||
| (8) |
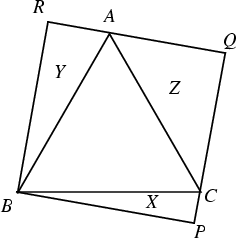
Let any Rectangle be circumscribed about an Equilateral Triangle. Then
| (9) |
Begin with an arbitrary Triangle and find the Excentral Triangle. Then find the Excentral Triangle of that triangle, and so on. Then the resulting triangle approaches an equilateral triangle. The only Rational Triangle is the equilateral triangle (Conway and Guy 1996). A Polyhedron composed of only equilateral triangles is known as a Deltahedron.
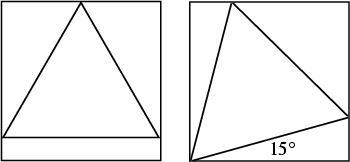
The smallest equilateral triangle which can be inscribed in a Unit Square (left figure) has side length and area
| (10) | |||
| (11) |
| (12) | |||
| (13) |
See also Acute Triangle, Deltahedron, Equilic Quadrilateral, Fermat Point, Gyroelongated Square Dipyramid, Icosahedron, Isogonic Centers, Isosceles Triangle, Morley's Theorem, Octahedron, Pentagonal Dipyramid, Right Triangle, Scalene Triangle, Snub Disphenoid, Tetrahedron, Triangle, Triangular Dipyramid, Triaugmented Triangular Prism, Viviani's Theorem
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 121, 1987.
Conway, J. H. and Guy, R. K. ``The Only Rational Triangle.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 201 and 228-239, 1996.
Dixon, R. Mathographics. New York: Dover, p. 33, 1991.
Gardner, M. Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American.
New York: Vintage Books, 1977.
Guy, R. K. ``Rational Distances from the Corners of a Square.'' §D19 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 181-185, 1994.
Honsberger, R. ``Equilateral Triangles.'' Ch. 3 in
Mathematical Gems I. Washington, DC: Math. Assoc. Amer., 1973.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 19-21, 1985.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 115 and 129-131, 1979.
|
|
|
© 1996-9 Eric W. Weisstein