|
|
|
|
The regular tetrahedron, often simply called ``the'' tetrahedron, is the Platonic Solid ![]() with four
Vertices, six Edges, and four equivalent
Equilateral Triangular faces
with four
Vertices, six Edges, and four equivalent
Equilateral Triangular faces ![]() . It is also Uniform Polyhedron
. It is also Uniform Polyhedron
![]() . It is described by the Schläfli Symbol
. It is described by the Schläfli Symbol ![]() and the Wythoff Symbol
is
and the Wythoff Symbol
is ![]() . It is the prototype of the Tetrahedral Group
. It is the prototype of the Tetrahedral Group ![]() ,
,
The tetrahedron is its own Dual Polyhedron. It is the only simple Polyhedron with no
Diagonals, and cannot be Stellated. The
Vertices of a tetrahedron are given by
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , or by (0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0). In the latter case, the face planes are
, or by (0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0). In the latter case, the face planes are
| (1) | |||
| (2) | |||
| (3) | |||
| (4) |
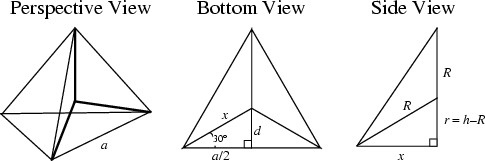
Let a tetrahedron be length ![]() on a side. The Vertices are located at (
on a side. The Vertices are located at (![]() , 0, 0),
(
, 0, 0),
(![]() ,
, ![]() , 0), and (0, 0,
, 0), and (0, 0, ![]() ). From the figure,
). From the figure,
| (5) |
 |
|||
| (6) |
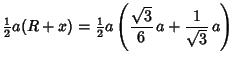 |
|||
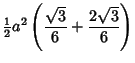 |
|||
 |
(7) |
| (8) |
| (9) |
| (10) |
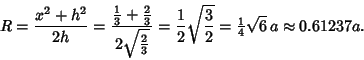 |
(11) |
| (12) |
| (13) |
| (14) |
| (15) |
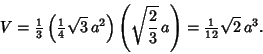 |
(16) |
| (17) |
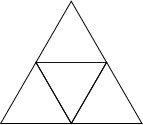
By slicing a tetrahedron as shown above, a Square can be obtained. This cut divides the tetrahedron into two congruent solids rotated by 90°.
Now consider a general (not necessarily regular) tetrahedron, defined as a convex Polyhedron consisting of four (not
necessarily identical) Triangular faces. Let the tetrahedron be specified by its
Vertices at ![]() where
where ![]() , ..., 4. Then the Volume is given by
, ..., 4. Then the Volume is given by
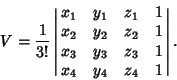 |
(18) |
| (19) |
| (20) |
| (21) | |||
| (22) | |||
| (23) |
| (24) |
The analog of Gauss's Circle Problem can be asked for tetrahedra: how many Lattice Points lie within a tetrahedron centered at the Origin with a given Inradius (Lehmer 1940, Granville 1991, Xu and Yau 1992, Guy 1994).
See also Augmented Truncated Tetrahedron, Bang's Theorem, Ehrhart Polynomial, Heronian Tetrahedron, Hilbert's 3rd Problem, Isosceles Tetrahedron, Sierpinski Tetrahedron, Stella Octangula, Tetrahedron 5-Compound, Tetrahedron 10-Compound, Truncated Tetrahedron
References
Davie, T. ``The Tetrahedron.''
http://www.dcs.st-and.ac.uk/~ad/mathrecs/polyhedra/tetrahedron.html.
Granville, A. ``The Lattice Points of an
Guy, R. K. ``Gauß's Lattice Point Problem.'' §F1 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 240-241, 1994.
Klee, V. and Wagon, S. Old and New Unsolved Problems in Plane Geometry and Number Theory, rev. ed.
Washington, DC: Math. Assoc. Amer., 1991.
Lehmer, D. H. ``The Lattice Points of an
Xu, Y. and Yau, S. ``A Sharp Estimate of the Number of Integral Points in a Tetrahedron.'' J. reine angew. Math.
423, 199-219, 1992.
![]() -Dimensional Tetrahedron.'' Aequationes Math. 41, 234-241, 1991.
-Dimensional Tetrahedron.'' Aequationes Math. 41, 234-241, 1991.
![]() -Dimensional Tetrahedron.'' Duke Math. J. 7, 341-353, 1940.
-Dimensional Tetrahedron.'' Duke Math. J. 7, 341-353, 1940.
|
|
|
© 1996-9 Eric W. Weisstein