The volume of a solid body is the amount of ``space'' it occupies. Volume has units of Length
cubed (i.e., cm3, m3, in3, etc.) For example, the volume of a box (Rectangular Parallelepiped) of
Length 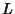 , Width
, Width 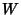 , and Height
, and Height  is given by
is given by
The volume can also be computed for irregularly-shaped and curved solids such as the Cylinder and
Cube. The volume of a Surface of Revolution is particularly simple to compute due to its symmetry.
The following table gives volumes for some common Surfaces. Here 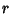 denotes
the Radius,
denotes
the Radius,  the height,
the height, 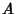 the base Area, and, in the case of the Torus,
the base Area, and, in the case of the Torus, 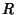 the
distance from the torus center to the center of the tube (Beyer 1987).
the
distance from the torus center to the center of the tube (Beyer 1987).
Even simple Surfaces can display surprisingly counterintuitive properties. For instance, the
Surface of Revolution of  around the
around the 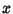 -axis for
-axis for 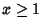 is called Gabriel's Horn, and has finite
volume, but infinite Surface Area.
is called Gabriel's Horn, and has finite
volume, but infinite Surface Area.
The generalization of volume to  Dimensions for
Dimensions for 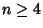 is known as Content.
is known as Content.
See also Arc Length, Area, Content, Height, Length (Size), Surface Area,
Surface of Revolution, Volume Element, Width (Size)
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press,
pp. 127-132, 1987.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , Width
, Width ![]() , and Height
, and Height ![]() is given by
is given by
![]()
![]() denotes
the Radius,
denotes
the Radius, ![]() the height,
the height, ![]() the base Area, and, in the case of the Torus,
the base Area, and, in the case of the Torus, ![]() the
distance from the torus center to the center of the tube (Beyer 1987).
the
distance from the torus center to the center of the tube (Beyer 1987).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() around the
around the ![]() -axis for
-axis for ![]() is called Gabriel's Horn, and has finite
volume, but infinite Surface Area.
is called Gabriel's Horn, and has finite
volume, but infinite Surface Area.
![]() Dimensions for
Dimensions for ![]() is known as Content.
is known as Content.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()