|
|
|
|
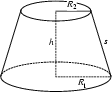
A conical frustum is a Frustum created by slicing the top off a Cone (with the cut made parallel to the base).
For a right circular Cone, let ![]() be the slant height and
be the slant height and ![]() and
and ![]() the top and bottom Radii.
Then
the top and bottom Radii.
Then
| (1) |
| (2) |
The Volume of the frustum is given by
| (3) |
| (4) |
![$\displaystyle \pi \int_0^h \left[{R_1+(R_2-R_1){z\over h}}\right]^2\,dz$](c2_1311.gif) |
|||
| (5) |
| (6) |
| (7) |
| (8) |
See also Cone, Frustum, Pyramidal Frustum, Spherical Segment
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed.
Boca Raton, FL: CRC Press, pp. 129-130 and 133, 1987.
|
|
|
© 1996-9 Eric W. Weisstein