The Surface of Revolution of the function  about the
about the  -axis for
-axis for 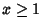 . It has Finite
Volume
. It has Finite
Volume
but Infinite Surface Area, since
This leads to the paradoxical consequence that while Gabriel's horn can be filled up with 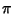 cubic units of paint,
an Infinite number of square units of paint are needed to cover its surface!
cubic units of paint,
an Infinite number of square units of paint are needed to cover its surface!
See also Funnel, Pseudosphere
© 1996-9 Eric W. Weisstein
1999-05-25
![]() about the
about the ![]() -axis for
-axis for ![]() . It has Finite
Volume
. It has Finite
Volume

![$\displaystyle \pi\left[{-{1\over x}}\right]_1^\infty =\pi[0-(-1)]=\pi,$](g_35.gif)
![\begin{eqnarray*}
S&=&\int_1^\infty 2\pi y\sqrt{1+{y'}^2}\,dx\\
&>& 2\pi\int_...
...over x} = 2\pi[\ln x]^\infty_1\\
&=& 2\pi[\ln\infty-0]=\infty.
\end{eqnarray*}](g_36.gif)