|
|
|

A Point at the intersection of two or more grid lines in a ruled array. (The array of grid lines could be oriented
to form unit cells in the shape of a square, rectangle, hexagon, etc.) However, unless otherwise specified, lattice points
are generally taken to refer to points in a square array, i.e., points with coordinates
![]() , where
, where ![]() ,
, ![]() ,
... are Integers.
,
... are Integers.
An ![]() -D
-D
![]() -lattice
-lattice ![]() lattice can be formally defined as a free
lattice can be formally defined as a free
![]() -Module in complex
-Module in complex
![]() -D space
-D space ![]() .
.
The Fraction of lattice points Visible from the
Origin, as derived in Castellanos (1988, pp. 155-156), is
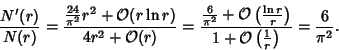
For
![]() , it is possible to select
, it is possible to select ![]() lattice points with
lattice points with ![]() such that no three are in a straight
Line. The number of distinct solutions (not counting reflections and rotations) for
such that no three are in a straight
Line. The number of distinct solutions (not counting reflections and rotations) for ![]() , 2, ..., are 1, 1, 4, 5,
11, 22, 57, 51, 156 ... (Sloane's A000769). For large
, 2, ..., are 1, 1, 4, 5,
11, 22, 57, 51, 156 ... (Sloane's A000769). For large ![]() , it is conjectured that it is only possible to select at most
, it is conjectured that it is only possible to select at most
![]() lattice points with no three Collinear, where
lattice points with no three Collinear, where
A special set of Polygons defined on the regular lattice are the Golygons. A Necessary and Sufficient condition that a linear transformation transforms a lattice to itself is that it be Unimodular. M. Ajtai has shown that there is no efficient Algorithm for finding any fraction of a set of spanning vectors in a lattice having the shortest lengths unless there is an efficient algorithm for all of them (of which none is known). This result has potential applications to cryptography and authentication (Cipra 1996).
See also Barnes-Wall Lattice, Blichfeldt's Theorem, Browkin's Theorem, Circle Lattice Points, Coxeter-Todd Lattice, Ehrhart Polynomial, Gauss's Circle Problem, Golygon, Integration Lattice, Jarnick's Inequality, Lattice Path, Lattice Sum, Leech Lattice, Minkowski Convex Body Theorem, Modular Lattice, N-Cluster, Nosarzewska's Inequality, Pick's Theorem, Poset, Random Walk, Schinzel's Theorem, Schröder Number, Visible Point, Voronoi Polygon
References
Apostol, T. Introduction to Analytic Number Theory. New York: Springer-Verlag, 1995.
Castellanos, D. ``The Ubiquitous Pi.'' Math. Mag. 61, 67-98, 1988.
Cipra, B. ``Lattices May Put Security Codes on a Firmer Footing.'' Science 273, 1047-1048, 1996.
Eppstein, D. ``Lattice Theory and Geometry of Numbers.''
http://www.ics.uci.edu/~eppstein/junkyard/lattice.html.
Guy, R. K. ``Gauß's Lattice Point Problem,'' ``Lattice Points with Distinct Distances,'' ``Lattice Points,
No Four on a Circle,'' and ``The No-Three-in-a-Line Problem.'' §F1, F2, F3, and F4 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 240-244, 1994.
Guy, R. K. and Kelly, P. A. ``The No-Three-in-Line-Problem.'' Canad. Math. Bull. 11, 527-531, 1968.
Hammer, J. Unsolved Problems Concerning Lattice Points. London: Pitman, 1977.
Sloane, N. J. A. Sequence
A000769/M3252
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein