|
|
|
Two Lattice Points ![]() and
and ![]() are mutually visible if the line segment joining them
contains no further Lattice Points. This corresponds to the requirement that
are mutually visible if the line segment joining them
contains no further Lattice Points. This corresponds to the requirement that ![]() ,
where
,
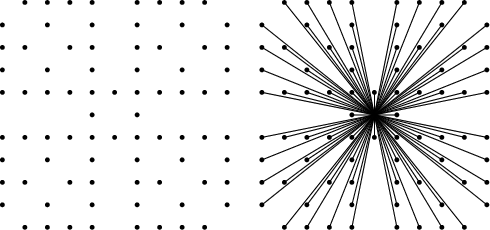
where ![]() denotes the Greatest Common Divisor. The plots above show the first few points visible from the
Origin.
denotes the Greatest Common Divisor. The plots above show the first few points visible from the
Origin.
If a Lattice Point is selected at random in 2-D, the probability that it is visible from the origin is ![]() .
This is also the probability that two Integers picked at random are Relatively Prime. If a
Lattice Point is picked at random in
.
This is also the probability that two Integers picked at random are Relatively Prime. If a
Lattice Point is picked at random in ![]() -D, the probability that it is visible from the Origin is
-D, the probability that it is visible from the Origin is
![]() , where
, where ![]() is the Riemann Zeta Function.
is the Riemann Zeta Function.
An invisible figure is a Polygon all of whose corners are invisible. There are invisible sets of every finite
shape. The lower left-hand corner of the invisible squares with smallest ![]() coordinate of Areas 2 and 3
are (14, 20) and (104, 6200).
coordinate of Areas 2 and 3
are (14, 20) and (104, 6200).
See also Lattice Point, Orchard Visibility Problem, Riemann Zeta Function
References
Apostol, T. §3.8 in Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
Baake, M.; Grimm, U.; and Warrington, D. H. ``Some Remarks on the Visible Points of a Lattice.''
J. Phys. A: Math. General 27, 2669-2674, 1994.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT
Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Herzog, F. and Stewart, B. M. ``Patterns of Visible and Nonvisible Lattice Points.'' Amer. Math. Monthly 78, 487-496, 1971.
Mosseri, R. ``Visible Points in a Lattice.'' J. Phys. A: Math. Gen. 25, L25-L29, 1992.
Schroeder, M. R. ``A Simple Function and Its Fourier Transform.'' Math. Intell. 4, 158-161, 1982.
Schroeder, M. R. Number Theory in Science and Communication, 2nd ed. New York: Springer-Verlag, 1990
|
|
|
© 1996-9 Eric W. Weisstein