|
|
|
A closed plane figure with ![]() sides. If all sides and angles are equivalent, the polygon is called regular. Regular polygons
can be Convex or Star. The word derives from the Greek poly (many) and
gonu (knee).
sides. If all sides and angles are equivalent, the polygon is called regular. Regular polygons
can be Convex or Star. The word derives from the Greek poly (many) and
gonu (knee).
The Area of a Convex Polygon with Vertices ![]() , ...,
, ..., ![]() is
is
| (1) |
| (2) |
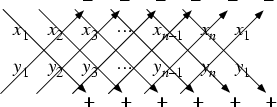
The Area of a polygon is defined to be Positive if the points are arranged in a counterclockwise order, and Negative if they are in clockwise order (Beyer 1987).
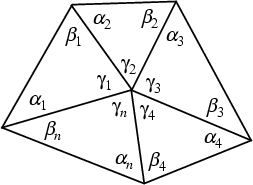
The sum ![]() of internal angles in the above diagram of a dissected polygon is
of internal angles in the above diagram of a dissected polygon is
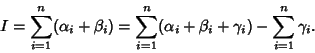 |
(3) |
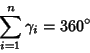 |
(4) |
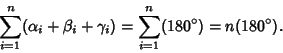 |
(5) |
| (6) |
Let ![]() be the number of sides. The regular
be the number of sides. The regular ![]() -gon is then denoted
-gon is then denoted ![]() .
.
| 2 | Digon |
| 3 | Equilateral Triangle (Trigon) |
| 4 | Square (Quadrilateral, Tetragon) |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| 9 | Nonagon (Enneagon) |
| 10 | Decagon |
| 11 | Undecagon (Hendecagon) |
| 12 | Dodecagon |
| 13 | Tridecagon (Triskaidecagon) |
| 14 | Tetradecagon (Tetrakaidecagon) |
| 15 | Pentadecagon (Pentakaidecagon) |
| 16 | Hexadecagon (Hexakaidecagon) |
| 17 | Heptadecagon (Heptakaidecagon) |
| 18 | Octadecagon (Octakaidecagon) |
| 19 | Enneadecagon (Enneakaidecagon) |
| 20 | Icosagon |
| 30 | Triacontagon |
| 40 | Tetracontagon |
| 50 | Pentacontagon |
| 60 | Hexacontagon |
| 70 | Heptacontagon |
| 80 | Octacontagon |
| 90 | Enneacontagon |
| 100 | Hectogon |
| 10000 | Myriagon |

Let ![]() be the side length,
be the side length, ![]() be the Inradius, and
be the Inradius, and ![]() the Circumradius. Then
the Circumradius. Then
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
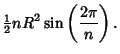 |
(12) |
 |
(13) | ||
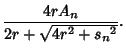 |
(14) |
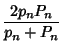 |
(15) | ||
| (16) |
| (17) | |||
 |
(18) |
Compass and Straightedge constructions dating back to Euclid ![]() were capable of inscribing regular
polygons of 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 40, 48, 64, ..., sides. However, this listing is not a complete
enumeration of ``constructible'' polygons. In fact, a regular
were capable of inscribing regular
polygons of 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 40, 48, 64, ..., sides. However, this listing is not a complete
enumeration of ``constructible'' polygons. In fact, a regular ![]() -gon is constructible only if
-gon is constructible only if ![]() is a Power
of 2, where
is a Power
of 2, where ![]() is the Totient Function (this is a Necessary but not Sufficient condition). More
specifically, a regular
is the Totient Function (this is a Necessary but not Sufficient condition). More
specifically, a regular ![]() -gon (
-gon (![]() ) can be constructed by Straightedge and Compass (i.e., can have
trigonometric functions of its Angles expressed in terms of finite Square Root extractions)
Iff
) can be constructed by Straightedge and Compass (i.e., can have
trigonometric functions of its Angles expressed in terms of finite Square Root extractions)
Iff
| (19) |
| (20) |
The fact that this condition was Sufficient was first proved by Gauß ![]() in 1796 when he was 19 years old, and
it relies on the property of Irreducible Polynomials that Roots composed of a
finite number of Square Root extractions exist only if the order of the equation is of the form
in 1796 when he was 19 years old, and
it relies on the property of Irreducible Polynomials that Roots composed of a
finite number of Square Root extractions exist only if the order of the equation is of the form ![]() . That this
condition was also Necessary was not explicitly proven by Gauss, and the first proof of this fact is credited to Wantzel
(1836).
. That this
condition was also Necessary was not explicitly proven by Gauss, and the first proof of this fact is credited to Wantzel
(1836).
Constructible values of ![]() for
for ![]() were given by Gauss (Smith 1994), and the first few are 2, 3, 4, 5, 6, 8, 10, 12,
15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, ...
(Sloane's A003401). Gardner (1977) and independently Watkins (Conway and Guy 1996) noticed that the number of sides for
constructible polygons with an Odd number of sides is given by the first 32 rows of Pascal's Triangle (mod 2)
interpreted as Binary numbers, giving 1, 3, 5, 15, 17, 51, 85, 255, ... (Sloane's A004729, Conway and
Guy 1996, p. 140).
were given by Gauss (Smith 1994), and the first few are 2, 3, 4, 5, 6, 8, 10, 12,
15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, ...
(Sloane's A003401). Gardner (1977) and independently Watkins (Conway and Guy 1996) noticed that the number of sides for
constructible polygons with an Odd number of sides is given by the first 32 rows of Pascal's Triangle (mod 2)
interpreted as Binary numbers, giving 1, 3, 5, 15, 17, 51, 85, 255, ... (Sloane's A004729, Conway and
Guy 1996, p. 140).

Although constructions for the regular Triangle, Square, Pentagon, and their derivatives had been
given by Euclid, ![]() constructions based on the Fermat Primes
constructions based on the Fermat Primes ![]() were unknown to the
ancients. The first explicit construction of a Heptadecagon (17-gon) was given by Erchinger in about 1800. Richelot
and Schwendenwein found constructions for the 257-gon in 1832, and Hermes spent 10 years on the construction of the
65537-gon at Göttingen around 1900 (Coxeter 1969). Constructions for the Equilateral Triangle and
Square are trivial (top figures below). Elegant constructions for the Pentagon and Heptadecagon are
due to Richmond (1893) (bottom figures below).
were unknown to the
ancients. The first explicit construction of a Heptadecagon (17-gon) was given by Erchinger in about 1800. Richelot
and Schwendenwein found constructions for the 257-gon in 1832, and Hermes spent 10 years on the construction of the
65537-gon at Göttingen around 1900 (Coxeter 1969). Constructions for the Equilateral Triangle and
Square are trivial (top figures below). Elegant constructions for the Pentagon and Heptadecagon are
due to Richmond (1893) (bottom figures below).

Given a point, a Circle may be constructed of any desired Radius, and a Diameter drawn through the
center. Call the center ![]() , and the right end of the Diameter
, and the right end of the Diameter ![]() . The Diameter Perpendicular to
the original Diameter may be constructed by finding the Perpendicular Bisector. Call the upper endpoint of
this Perpendicular Diameter
. The Diameter Perpendicular to
the original Diameter may be constructed by finding the Perpendicular Bisector. Call the upper endpoint of
this Perpendicular Diameter ![]() . For the Pentagon, find the Midpoint of
. For the Pentagon, find the Midpoint of ![]() and call it
and call it ![]() .
Draw
.
Draw ![]() , and Bisect
, and Bisect ![]() , calling the intersection point with
, calling the intersection point with ![]()
![]() . Draw
. Draw
![]() Parallel to
Parallel to ![]() , and the first two points of the Pentagon are
, and the first two points of the Pentagon are ![]() and
and ![]() . The construction
for the Heptadecagon is more complicated, but can be accomplished in 17 relatively simple steps. The construction
problem has now been automated (Bishop 1978).
. The construction
for the Heptadecagon is more complicated, but can be accomplished in 17 relatively simple steps. The construction
problem has now been automated (Bishop 1978).
See also 257-gon, 65537-gon, Anthropomorphic Polygon, Bicentric Polygon, Carnot's Polygon Theorem, Chaos Game, Convex Polygon, Cyclic Polygon, de Moivre Number, Diagonal (Polygon), Equilateral Triangle, Euler's Polygon Division Problem, Heptadecagon, Hexagon, Hexagram, Illumination Problem, Jordan Polygon, Lozenge, Octagon, Parallelogram, Pascal's Theorem, Pentagon, Pentagram, Petrie Polygon, Polygon Circumscribing Constant, Polygon Inscribing Constant, Polygonal Knot, Polygonal Number, Polygonal Spiral, Polygon Triangulation, Polygram, Polyhedral Formula, Polyhedron, Polytope, Quadrangle, Quadrilateral, Regular Polygon, Reuleaux Polygon, Rhombus, Rotor, Simple Polygon, Simplicity, Square, Star Polygon, Trapezium, Trapezoid, Triangle, Visibility, Voronoi Polygon, Wallace-Bolyai-Gerwein Theorem
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 124-125 and 196, 1987.
Bishop, W. ``How to Construct a Regular Polygon.'' Amer. Math. Monthly 85, 186-188, 1978.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 140 and 197-202, 1996.
Courant, R. and Robbins, H. ``Regular Polygons.'' §3.2 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 122-125, 1996.
Coxeter, H. S.M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.
De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly
98, 97-108, 1991.
Gardner, M. Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American.
New York: Vintage Books, p. 207, 1977.
Gauss, C. F. §365 and 366 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801.
Translated by A. A Clarke. New Haven, CT: Yale University Press, 1965.
The Math Forum. ``Naming Polygons and Polyhedra.''
http://forum.swarthmore.edu/dr.math/faq/faq.polygon.names.html.
Rawles, B. Sacred Geometry Design Sourcebook: Universal Dimensional Patterns. Nevada City, CA: Elysian Pub., p. 238, 1997.
Richmond, H. W. ``A Construction for a Regular Polygon of Seventeen Sides.'' Quart. J. Pure Appl. Math. 26, 206-207, 1893.
Sloane, N. J. A. Sequences
A004729 and
A003401/M0505
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Smith, D. E. A Source Book in Mathematics. New York: Dover, p. 350, 1994.
Tietze, H. Ch. 9 in Famous Problems of Mathematics. New York: Graylock Press, 1965.
Wantzel, M. L. ``Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se
résoudre avec la règle et le compas.'' J. Math. pures appliq. 1, 366-372, 1836.
|
|
|
© 1996-9 Eric W. Weisstein