|
|
|
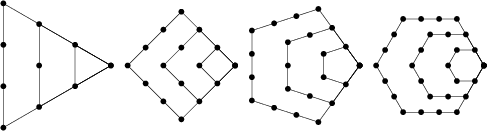
A type of Figurate Number which is a generalization of Triangular, Square, etc., numbers to an arbitrary ![]() -gonal number. The above diagrams graphically illustrate the process by which
the polygonal numbers are built up. Starting with the
-gonal number. The above diagrams graphically illustrate the process by which
the polygonal numbers are built up. Starting with the ![]() th Triangular Number
th Triangular Number ![]() , then
, then
| (1) |
| (2) |
| (3) |
| (4) |
Fermat ![]() proposed that every number is expressible as at most
proposed that every number is expressible as at most ![]()
![]() -gonal numbers (Fermat's Polygonal
Number Theorem). Fermat claimed to have a proof of this result, although this proof has never been found. Jacobi
-gonal numbers (Fermat's Polygonal
Number Theorem). Fermat claimed to have a proof of this result, although this proof has never been found. Jacobi ![]() ,
Lagrange
,
Lagrange ![]() (1772), and Euler
(1772), and Euler ![]() all proved the square case, and Gauß
all proved the square case, and Gauß ![]() proved the triangular case in
1796. In 1813, Cauchy
proved the triangular case in
1796. In 1813, Cauchy ![]() proved the proposition in its entirety.
proved the proposition in its entirety.
An arbitrary number ![]() can be checked to see if it is a
can be checked to see if it is a ![]() -gonal number as follows. Note the identity
-gonal number as follows. Note the identity
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
| (6) |
| (7) |
See also Centered Polygonal Number, Decagonal Number, Fermat's Polygonal Number Theorem, Figurate Number, Heptagonal Number, Hexagonal Number, Nonagonal Number, Octagonal Number, Pentagonal Number, Pyramidal Number, Square Number, Triangular Number
References
Beiler, A. H. ``Ball Games.'' Ch. 18 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains.
New York: Dover, pp. 184-199, 1966.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 3-33, 1952.
Guy, K. ``Every Number is Expressible as a Sum of How Many Polygonal Numbers?'' Amer. Math. Monthly 101, 169-172, 1994.
Pappas, T. ``Triangular, Square & Pentagonal Numbers.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, p. 214, 1989.
Sloane, N. J. A. Sequence
A000217/M2535
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in
Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein