|
|
|
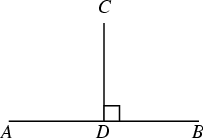
Two lines, vectors, planes, etc., are said to be perpendicular if they meet at a Right Angle. In ![]() , two
Vectors
, two
Vectors ![]() and
and ![]() are Perpendicular if their Dot Product
are Perpendicular if their Dot Product
In the above figure, the Line Segment ![]() is perpendicular to the Line Segment
is perpendicular to the Line Segment ![]() . This relationship
is commonly denoted with a small Square at the vertex where perpendicular objects meet, as shown above, and is
denoted
. This relationship
is commonly denoted with a small Square at the vertex where perpendicular objects meet, as shown above, and is
denoted ![]() .
.
See also Orthogonal Vectors, Parallel, Perpendicular Bisector, Perpendicular Foot, Right Angle