|
|
|

A square root of ![]() is a number
is a number ![]() such that
such that ![]() . This is written
. This is written ![]() (
(![]() to the 1/2 Power) or
to the 1/2 Power) or
![]() . The square root function
. The square root function ![]() is the Inverse Function of
is the Inverse Function of ![]() . Square roots are also
called Radicals or Surds. A general Complex Number
. Square roots are also
called Radicals or Surds. A general Complex Number ![]() has two square
roots. For example, for the real Positive number
has two square
roots. For example, for the real Positive number ![]() , the two square roots are
, the two square roots are
![]() , since
, since
![]() . Similarly, for the real Negative number
. Similarly, for the real Negative number ![]() , the two square roots are
, the two square roots are
![]() , where
i is the Imaginary Number defined by
, where
i is the Imaginary Number defined by ![]() . In common usage, unless otherwise specified, ``the'' square
root is generally taken to mean the Positive square root.
. In common usage, unless otherwise specified, ``the'' square
root is generally taken to mean the Positive square root.
The square root of 2 is the Irrational Number
![]() (Sloane's A002193), which has the simple periodic
Continued Fraction 1, 2, 2, 2, 2, 2, .... The square root of 3 is the Irrational Number
(Sloane's A002193), which has the simple periodic
Continued Fraction 1, 2, 2, 2, 2, 2, .... The square root of 3 is the Irrational Number
![]() (Sloane's A002194), which has the simple periodic Continued Fraction 1, 1, 2, 1, 2, 1, 2, .... In general,
the Continued Fractions of the square roots of all Positive integers are periodic.
(Sloane's A002194), which has the simple periodic Continued Fraction 1, 1, 2, 1, 2, 1, 2, .... In general,
the Continued Fractions of the square roots of all Positive integers are periodic.
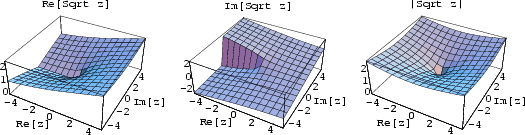
The square roots of a Complex Number are given by
| (1) |
A Nested Radical of the form
![]() can sometimes be simplified into a simple square root
by equating
can sometimes be simplified into a simple square root
by equating
| (2) |
| (3) |
| (4) | |||
| (5) |
| (6) |
A sequence of approximations ![]() to
to ![]() can be derived by factoring
can be derived by factoring
| (7) |
| (8) |
| (9) |
| (10) | |||
| (11) | |||
| (12) |
| (13) | |||
| (14) |
| (15) |
| (16) |
Another general technique for deriving this sequence, known as Newton's Iteration, is obtained by letting ![]() .
Then
.
Then ![]() , so the Sequence
, so the Sequence
| (17) |
| (18) |
See also Continued Square Root, Cube Root, Nested Radical, Newton's Iteration, Quadratic Surd, Root of Unity, Square Number, Square Triangular Number, Surd
References
Sloane, N. J. A. Sequences
A002193/M3195
and A002194/M4326
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Spanier, J. and Oldham, K. B. ``The Square-Root Function
Williams, H. C. ``A Numerical Investigation into the Length of the Period of the Continued Fraction Expansion of
![]() and Its Reciprocal,''
``The
and Its Reciprocal,''
``The
![]() Function and Its Reciprocal,'' and ``The
Function and Its Reciprocal,'' and ``The ![]() Function.''
Chs. 12, 14, and 15 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 91-99, 107-115, and 115-122, 1987.
Function.''
Chs. 12, 14, and 15 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 91-99, 107-115, and 115-122, 1987.
![]() .''
Math. Comp. 36, 593-601, 1981.
.''
Math. Comp. 36, 593-601, 1981.
|
|
|
© 1996-9 Eric W. Weisstein