A ``general'' continued fraction representation of a Real Number  is of the form
is of the form
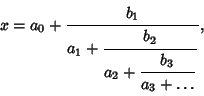 |
(1) |
which can be written
 |
(2) |
The Simple Continued Fraction representation of  (which is usually what is meant when the term ``continued
fraction'' is used without qualification) of a number is given by
(which is usually what is meant when the term ``continued
fraction'' is used without qualification) of a number is given by
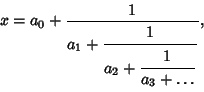 |
(3) |
which can be written in a compact abbreviated Notation as
![\begin{displaymath}
x=[a_0, a_1, a_2, a_3, \ldots].
\end{displaymath}](c2_1452.gif) |
(4) |
Here,
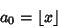 |
(5) |
is the integral part of  (where
(where
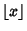 is the Floor Function),
is the Floor Function),
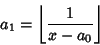 |
(6) |
is the integral part of the Reciprocal of  ,
, 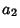 is the integral part of the reciprocal of the
remainder, etc. The quantities
is the integral part of the reciprocal of the
remainder, etc. The quantities 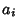 are called Partial Quotients. An archaic word for a
continued fraction is Anthyphairetic Ratio.
are called Partial Quotients. An archaic word for a
continued fraction is Anthyphairetic Ratio.
Continued fractions provide, in some sense, a series of ``best'' estimates for an Irrational Number. Functions can
also be written as continued fractions, providing a series of better and better rational approximations. Continued fractions
have also proved useful in the proof of certain properties of numbers such as e and 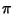 (Pi). Because
irrationals which are square roots of Rational Numbers have periodic continued fractions, an exact
representation for a tabulated numerical value (i.e., 1.414... for Pythagoras's Constant,
(Pi). Because
irrationals which are square roots of Rational Numbers have periodic continued fractions, an exact
representation for a tabulated numerical value (i.e., 1.414... for Pythagoras's Constant, 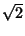 ) can
sometimes be found.
) can
sometimes be found.
Continued fractions are also useful for finding near commensurabilities between events with different periods. For example,
the Metonic cycle  used for calendrical purposes by the Greeks consists of 235 lunar months
which very nearly equal 19 solar years, and 235/19 is the sixth Convergent of the ratio of the lunar phase (synodic)
period and solar period (365.2425/29.53059). Continued fractions can also be used to calculate gear ratios, and were used
for this purpose by the ancient Greeks (Guy 1990).
used for calendrical purposes by the Greeks consists of 235 lunar months
which very nearly equal 19 solar years, and 235/19 is the sixth Convergent of the ratio of the lunar phase (synodic)
period and solar period (365.2425/29.53059). Continued fractions can also be used to calculate gear ratios, and were used
for this purpose by the ancient Greeks (Guy 1990).
If only the first few terms of a continued fraction are kept, the result is called a Convergent. Let 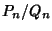 be
convergents of a nonsimple continued fraction. Then
be
convergents of a nonsimple continued fraction. Then
 |
(7) |
 |
(8) |
and subsequent terms are calculated from the Recurrence Relations
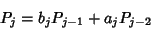 |
(9) |
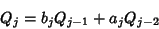 |
(10) |
for 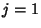 , 2, ...,
, 2, ..., 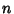 . It is also true that
. It is also true that
 |
(11) |
The error in approximating a number by a given Convergent is roughly the Multiplicative Inverse of the square
of the Denominator of the first neglected term.
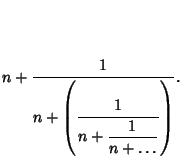
A finite simple continued fraction representation terminates after a finite number of terms. To ``round'' a
continued fraction, truncate the last term unless it is 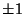 , in which case it should be added to the previous term
(Beeler et al. 1972, Item 101A). To take one over a continued fraction, add (or possibly delete) an initial 0 term. To
negate, take the Negative of all terms, optionally using the identity
, in which case it should be added to the previous term
(Beeler et al. 1972, Item 101A). To take one over a continued fraction, add (or possibly delete) an initial 0 term. To
negate, take the Negative of all terms, optionally using the identity
![\begin{displaymath}[-a, -b, -c, -d, \ldots]=[-a-1, 1, b-1, c, d, \ldots].
\end{displaymath}](c2_1466.gif) |
(12) |
A particularly beautiful identity involving the terms of the continued fraction is
![\begin{displaymath}
{[a_0, a_1, \ldots, a_n]\over[a_0, a_1, \ldots, a_{n-1}]}
=...
... a_{n-1}, \ldots, a_1, a_0]\over [a_n, a_{n-1}, \ldots, a_1]}.
\end{displaymath}](c2_1467.gif) |
(13) |
Finite simple fractions represent rational numbers and all rational numbers are represented by finite continued
fractions. There are two possible representations for a finite simple fraction:
![\begin{displaymath}[a_0, \ldots, a_n]=\cases{
[a_0, \ldots, a_{n-1}, a_n-1, 1] &...
...a_n>1$\cr
[a_0, \ldots, a_{n-2}, a_{n-1}+1] & for $a_n=1$.\cr}
\end{displaymath}](c2_1468.gif) |
(14) |
On the other hand, an infinite simple fraction represents a unique Irrational Number, and each Irrational
Number has a unique infinite continued fraction.
Consider the Convergents 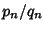 of a simple continued fraction, and define
of a simple continued fraction, and define
 |
(15) |
 |
(16) |
 |
(17) |
Then subsequent terms can be calculated from the Recurrence Relations
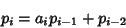 |
(18) |
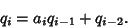 |
(19) |
The Continued Fraction Fundamental Recurrence Relation for simple continued fractions is
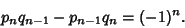 |
(20) |
It is also true that if 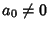 ,
,
Furthermore,
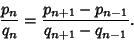 |
(23) |
Also, if a convergent 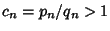 , then
, then
![\begin{displaymath}
{q_n\over p_n}=[0, a_0, a_1, \ldots, a_n].
\end{displaymath}](c2_1483.gif) |
(24) |
Similarly, if 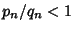 , then
, then
![\begin{displaymath}
{q_n\over p_n}=[a_0, a_1, \ldots, a_n].
\end{displaymath}](c2_1485.gif) |
(25) |
The convergents 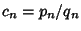 also satisfy
also satisfy
The Even convergents 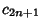 of an infinite simple continued fraction form an Increasing Sequence, and the
Odd convergents
of an infinite simple continued fraction form an Increasing Sequence, and the
Odd convergents  form a Decreasing Sequence (so any Even convergent is less than any Odd
convergent). Summarizing,
form a Decreasing Sequence (so any Even convergent is less than any Odd
convergent). Summarizing,
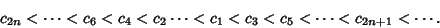 |
(28) |
Furthermore, each convergent for 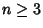 lies between the two preceding ones. Each convergent is nearer to the value of
the infinite continued fraction than the previous one. In addition, for a number
lies between the two preceding ones. Each convergent is nearer to the value of
the infinite continued fraction than the previous one. In addition, for a number
![$x=[a_0,a_1,\dots]$](c2_1494.gif) ,
,
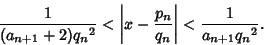 |
(29) |
The Square Root of a Squarefree Integer has a periodic continued fraction of the form
![\begin{displaymath}
\sqrt{n}=[a_0, \overline{a_1, \ldots, a_n, 2a_0}\,]
\end{displaymath}](c2_1496.gif) |
(30) |
(Rose 1994, p. 130). Furthermore, if 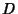 is not a Square Number, then the terms of the continued fraction of
is not a Square Number, then the terms of the continued fraction of
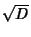 satisfy
satisfy
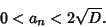 |
(31) |
In particular,
![\begin{displaymath}[\overline{a_1, \ldots, a_n}]= {-(q_{n-1}-p_n)+\sqrt{(q_{n-1}-p_n)^2+4q_np_{n-1}}\over 2q_n}
\end{displaymath}](c2_1503.gif) |
(36) |
The first follows from
Therefore,
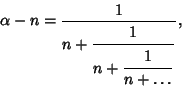 |
(40) |
so plugging (40) into (39) gives
 |
(41) |
Expanding
 |
(42) |
and solving using the Quadratic Formula gives
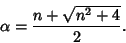 |
(43) |
The analog of this treatment in the general case gives
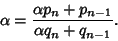 |
(44) |
The following table gives the repeating simple continued fractions for the square roots of the first few integers (excluding
the trivial Square Numbers).
 |
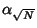 |
 |
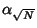 |
| 2 |
![$[1, \overline{2}]$](c2_1516.gif) |
22 |
![$[4, \overline{1, 2, 4, 2, 1, 8}]$](c2_1517.gif) |
| 3 |
![$[1, \overline{1, 2}]$](c2_1518.gif) |
23 |
![$[4, \overline{1, 3, 1, 8}]$](c2_1519.gif) |
| 5 |
![$[2, \overline{4}]$](c2_1520.gif) |
24 |
![$[4, \overline{1, 8}]$](c2_1521.gif) |
| 6 |
![$[2, \overline{2, 4}]$](c2_1522.gif) |
26 |
![$[5, \overline{10}]$](c2_1523.gif) |
| 7 |
![$[2, \overline{1, 1, 1, 4}]$](c2_1524.gif) |
27 |
![$[5, \overline{5, 10}]$](c2_1525.gif) |
| 8 |
![$[2, \overline{1, 4}]$](c2_1526.gif) |
28 |
![$[5, \overline{3, 2, 3, 10}]$](c2_1527.gif) |
| 10 |
![$[3, \overline{6}]$](c2_1528.gif) |
29 |
![$[5, \overline{2, 1, 1, 2, 10}]$](c2_1529.gif) |
| 11 |
![$[3, \overline{3, 6}]$](c2_1530.gif) |
30 |
![$[5, \overline{2, 10}]$](c2_1531.gif) |
| 12 |
![$[3, \overline{2, 6}]$](c2_1532.gif) |
31 |
![$[5, \overline{1, 1, 3, 5, 3, 1, 1, 10}]$](c2_1533.gif) |
| 13 |
![$[3, \overline{1, 1, 1, 1, 6}]$](c2_1534.gif) |
32 |
![$[5, \overline{1, 1, 1, 10}]$](c2_1535.gif) |
| 14 |
![$[3, \overline{1, 2, 1, 6}]$](c2_1536.gif) |
33 |
![$[5, \overline{1, 2, 1, 10}]$](c2_1537.gif) |
| 15 |
![$[3, \overline{1, 6}]$](c2_1538.gif) |
34 |
![$[5, \overline{1, 4, 1, 10}]$](c2_1539.gif) |
| 17 |
![$[4, \overline{8}]$](c2_1540.gif) |
35 |
![$[5, \overline{1, 10}]$](c2_1541.gif) |
| 18 |
![$[4, \overline{4, 8}]$](c2_1542.gif) |
37 |
![$[6, \overline{12}]$](c2_1543.gif) |
| 19 |
![$[4, \overline{2, 1, 3, 1, 2, 8}]$](c2_1544.gif) |
38 |
![$[6, \overline{6, 12}]$](c2_1545.gif) |
| 20 |
![$[4, \overline{2, 8}]$](c2_1546.gif) |
39 |
![$[6, \overline{4, 12}]$](c2_1547.gif) |
| 21 |
![$[4, \overline{1, 1, 2, 1, 1, 8}]$](c2_1548.gif) |
40 |
![$[6, \overline{3, 12}]$](c2_1549.gif) |
The periods of the continued fractions of the square roots of the first few nonsquare integers 2, 3, 5, 6, 7, 8, 10,
11, 12, 13, ... (Sloane's A000037) are 1, 2, 1, 2, 4, 2, 1, 2, 2, 5, ... (Sloane's A013943; Williams 1981, Jacobson et al. 1995).
An upper bound for the length is roughly
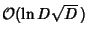 .
.
An even stronger result is that a continued fraction is periodic Iff it is a Root of a quadratic
Polynomial. Calling the portion of a number  remaining after a given convergent the ``tail,'' it must be true that
the relationship between the number
remaining after a given convergent the ``tail,'' it must be true that
the relationship between the number  and terms in its tail is of the form
and terms in its tail is of the form
 |
(45) |
which can only lead to a Quadratic Equation.
Logarithms
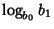 can be computed by defining
can be computed by defining  , ...and the Positive
Integer
, ...and the Positive
Integer 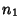 , ...such that
, ...such that
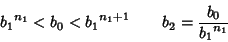 |
(46) |
 |
(47) |
and so on. Then
![\begin{displaymath}
\log_{b_0} b_1 = [n_1, n_2, n_3, \ldots].
\end{displaymath}](c2_1557.gif) |
(48) |
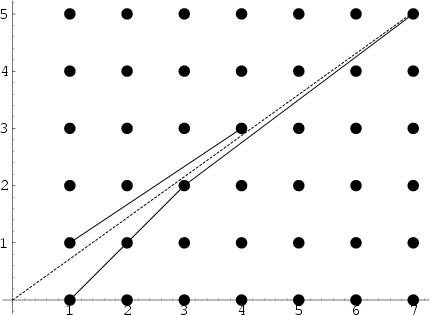
A geometric interpretation for a reduced Fraction 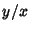 consists of a string through a Lattice of points with
ends at
consists of a string through a Lattice of points with
ends at  and
and 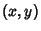 (Klein 1907, 1932; Steinhaus 1983; Ball and Coxeter 1987, pp. 86-87; Davenport 1992). This
interpretation is closely related to a similar one for the Greatest Common Divisor. The pegs it presses against
(Klein 1907, 1932; Steinhaus 1983; Ball and Coxeter 1987, pp. 86-87; Davenport 1992). This
interpretation is closely related to a similar one for the Greatest Common Divisor. The pegs it presses against
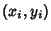 give alternate Convergents
give alternate Convergents  , while the other Convergents
are obtained from the pegs it presses against with the initial end at
, while the other Convergents
are obtained from the pegs it presses against with the initial end at 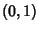 . The above plot is for
. The above plot is for  , which has
convergents 0, 1, 2/3, 3/4, 5/7, ....
, which has
convergents 0, 1, 2/3, 3/4, 5/7, ....
Let the continued fraction for  be written
be written
![$[a_0,a_1,a_2,\ldots,a_n]$](c2_1564.gif) . Then the limiting value is almost always
Khintchine's Constant
. Then the limiting value is almost always
Khintchine's Constant
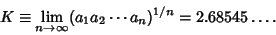 |
(49) |
Continued fractions can be used to express the Positive Roots of any Polynomial equation. Continued fractions
can also be used to solve linear Diophantine Equations and the Pell Equation.
Euler  showed that if a Convergent Series can be written in the form
showed that if a Convergent Series can be written in the form
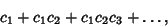 |
(50) |
then it is equal to the continued fraction
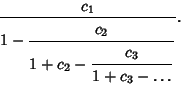 |
(51) |
Gosper has invented an Algorithm for performing analytic Addition, Subtraction, Multiplication,
and Division using continued fractions. It requires keeping track of eight Integers which are
conceptually arranged at the Vertices of a Cube. The Algorithm has not,
however, appeared in print (Gosper 1996).
An algorithm for computing the continued fraction for 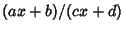 from the continued fraction for
from the continued fraction for  is given by
Beeler et al. (1972, Item 101), Knuth (1981, Exercise 4.5.3.15, pp. 360 and 601), and Fowler (1991). (In line 9 of Knuth's solution,
is given by
Beeler et al. (1972, Item 101), Knuth (1981, Exercise 4.5.3.15, pp. 360 and 601), and Fowler (1991). (In line 9 of Knuth's solution,
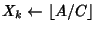 should be replaced by
should be replaced by
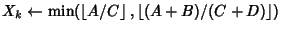 .)
Beeler et al. (1972) and
Knuth (1981) also mention the bivariate case
.)
Beeler et al. (1972) and
Knuth (1981) also mention the bivariate case
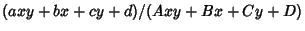 .
.
See also Gaussian Brackets, Hurwitz's Irrational Number Theorem, Khintchine's Constant, Lagrange's
Continued Fraction Theorem, Lamé's Theorem, Lévy Constant,
Padé Approximant, Partial Quotient, Pi, Quadratic Irrational Number,
Quotient-Difference Algorithm, Segre's Theorem
References
 Continued Fractions
Continued Fractions
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 19, 1972.
Acton, F. S. ``Power Series, Continued Fractions, and Rational Approximations.''
Ch. 11 in Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., 1990.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, pp. 54-57 and 86-87, 1987.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239,
pp. 36-44, Feb. 1972.
Beskin, N. M. Fascinating Fractions. Moscow: Mir Publishers, 1980.
Brezinski, C. History of Continued Fractions and Padé Approximants. New York: Springer-Verlag, 1980.
Conway, J. H. and Guy, R. K. ``Continued Fractions.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 176-179, 1996.
Courant, R. and Robbins, H. ``Continued Fractions. Diophantine Equations.'' §2.4 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 49-51, 1996.
Davenport, H. §IV.12 in The Higher Arithmetic: An Introduction to the Theory of Numbers, 6th ed.
New York: Cambridge University Press, 1992.
Euler, L. Introduction to Analysis of the Infinite, Book I. New York: Springer-Verlag, 1980.
Fowler, D. H. The Mathematics of Plato's Academy. Oxford, England: Oxford University Press, 1991.
Guy, R. K. ``Continued Fractions'' §F20 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 259, 1994.
Jacobson, M. J. Jr.; Lukes, R. F.; and Williams, H. C. ``An Investigation of Bounds for the Regulator of Quadratic Fields.''
Experiment. Math. 4, 211-225, 1995.
Khinchin, A. Ya. Continued Fractions. New York: Dover, 1997.
Kimberling, C. ``Continued Fractions.''
http://cedar.evansville.edu/~ck6/integer/contfr.html.
Klein, F. Ausgewählte Kapitel der Zahlentheorie. Germany: Teubner, 1907.
Klein, F. Elementary Number Theory. New York, p. 44, 1932.
Kline, M. Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press, 1972.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd ed.
Reading, MA: Addison-Wesley, p. 316, 1981.
Moore, C. D. An Introduction to Continued Fractions. Washington, DC: National
Council of Teachers of Mathematics, 1964.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Pettofrezzo, A. J. and Bykrit, D. R. Elements of Number Theory. Englewood Cliffs, NJ: Prentice-Hall, 1970.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Evaluation of Continued Fractions.'' §5.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 163-167, 1992.
Rose, H. E. A Course in Number Theory, 2nd ed. Oxford, England: Oxford University Press, 1994.
Rosen, K. H. Elementary Number Theory and Its Applications. New York: Addison-Wesley, 1980.
Sloane, N. J. A. Sequences
A013943 and
A000037/M0613
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Steinhaus, H. Mathematical Snapshots, 3rd American ed. New York: Oxford University Press, pp. 39-42, 1983.
Van Tuyl, A. L. ``Continued Fractions.'' http://www.calvin.edu/academic/math/confrac/.
Wagon, S. ``Continued Fractions.'' §8.5 in Mathematica in Action. New York: W. H. Freeman, pp. 263-271, 1991.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Williams, H. C. ``A Numerical Investigation into the Length of the Period of the Continued Fraction Expansion of 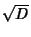 .''
Math. Comp. 36, 593-601, 1981.
.''
Math. Comp. 36, 593-601, 1981.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is of the form
is of the form
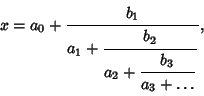
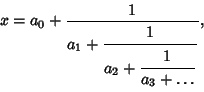
![]() (Pi). Because
irrationals which are square roots of Rational Numbers have periodic continued fractions, an exact
representation for a tabulated numerical value (i.e., 1.414... for Pythagoras's Constant,
(Pi). Because
irrationals which are square roots of Rational Numbers have periodic continued fractions, an exact
representation for a tabulated numerical value (i.e., 1.414... for Pythagoras's Constant, ![]() ) can
sometimes be found.
) can
sometimes be found.
![]() used for calendrical purposes by the Greeks consists of 235 lunar months
which very nearly equal 19 solar years, and 235/19 is the sixth Convergent of the ratio of the lunar phase (synodic)
period and solar period (365.2425/29.53059). Continued fractions can also be used to calculate gear ratios, and were used
for this purpose by the ancient Greeks (Guy 1990).
used for calendrical purposes by the Greeks consists of 235 lunar months
which very nearly equal 19 solar years, and 235/19 is the sixth Convergent of the ratio of the lunar phase (synodic)
period and solar period (365.2425/29.53059). Continued fractions can also be used to calculate gear ratios, and were used
for this purpose by the ancient Greeks (Guy 1990).
![]() be
convergents of a nonsimple continued fraction. Then
be
convergents of a nonsimple continued fraction. Then

![]() , in which case it should be added to the previous term
(Beeler et al. 1972, Item 101A). To take one over a continued fraction, add (or possibly delete) an initial 0 term. To
negate, take the Negative of all terms, optionally using the identity
, in which case it should be added to the previous term
(Beeler et al. 1972, Item 101A). To take one over a continued fraction, add (or possibly delete) an initial 0 term. To
negate, take the Negative of all terms, optionally using the identity
![]() of a simple continued fraction, and define
of a simple continued fraction, and define


![$\quad [\overline{a, b}] = {ab+\sqrt{ab(ab+4)}\over 2b}$](c2_1502.gif)
![$\displaystyle {[\overline{b_1, \ldots, b_n}] p_n+p_{n-1}\over [\overline{b_1, \ldots, b_n}] q_n+q_{n-1}}.$](c2_1507.gif)
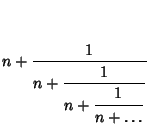
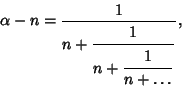
![]() .
.
![]() remaining after a given convergent the ``tail,'' it must be true that
the relationship between the number
remaining after a given convergent the ``tail,'' it must be true that
the relationship between the number ![]() and terms in its tail is of the form
and terms in its tail is of the form
![]() can be computed by defining
can be computed by defining ![]() , ...and the Positive
Integer
, ...and the Positive
Integer ![]() , ...such that
, ...such that
![]() consists of a string through a Lattice of points with
ends at
consists of a string through a Lattice of points with
ends at ![]() and
and ![]() (Klein 1907, 1932; Steinhaus 1983; Ball and Coxeter 1987, pp. 86-87; Davenport 1992). This
interpretation is closely related to a similar one for the Greatest Common Divisor. The pegs it presses against
(Klein 1907, 1932; Steinhaus 1983; Ball and Coxeter 1987, pp. 86-87; Davenport 1992). This
interpretation is closely related to a similar one for the Greatest Common Divisor. The pegs it presses against
![]() give alternate Convergents
give alternate Convergents ![]() , while the other Convergents
are obtained from the pegs it presses against with the initial end at
, while the other Convergents
are obtained from the pegs it presses against with the initial end at ![]() . The above plot is for
. The above plot is for ![]() , which has
convergents 0, 1, 2/3, 3/4, 5/7, ....
, which has
convergents 0, 1, 2/3, 3/4, 5/7, ....
![]() be written
be written
![]() . Then the limiting value is almost always
Khintchine's Constant
. Then the limiting value is almost always
Khintchine's Constant
![]() showed that if a Convergent Series can be written in the form
showed that if a Convergent Series can be written in the form
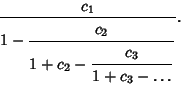
![]() from the continued fraction for
from the continued fraction for ![]() is given by
Beeler et al. (1972, Item 101), Knuth (1981, Exercise 4.5.3.15, pp. 360 and 601), and Fowler (1991). (In line 9 of Knuth's solution,
is given by
Beeler et al. (1972, Item 101), Knuth (1981, Exercise 4.5.3.15, pp. 360 and 601), and Fowler (1991). (In line 9 of Knuth's solution,
![]() should be replaced by
should be replaced by
![]() .)
Beeler et al. (1972) and
Knuth (1981) also mention the bivariate case
.)
Beeler et al. (1972) and
Knuth (1981) also mention the bivariate case
![]() .
.
![]() Continued Fractions
Continued Fractions
![]() .''
Math. Comp. 36, 593-601, 1981.
.''
Math. Comp. 36, 593-601, 1981.