Convergent

The Rational Number obtained by keeping only a limited number of terms in a Continued Fraction is called a convergent. For example, in the Simple Continued Fraction for the Golden Ratio,

$$\phi=1+{1\over\strut\displaystyle 1+{\strut\displaystyle 1\over\strut\displaystyle 1+\ldots}},$$

the convergents are

$$1, 1+{1\over 1}=2, 1+{1\over 1+{1\over 1}}={3\over 2}, \ldots.$$

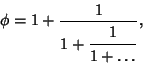
The word convergent is also used to describe a Convergent Sequence or Convergent Series.

See also Continued Fraction, Convergent Sequence, Convergent Series, Partial Quotient, Simple Continued Fraction