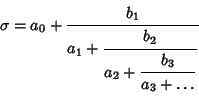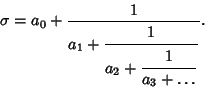A Continued Fraction
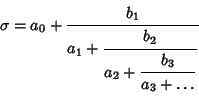 |
(1) |
in which the 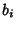 s are all unity, leaving a continued fraction of the form
s are all unity, leaving a continued fraction of the form
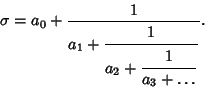 |
(2) |
A simple continued fraction can be written in a compact abbreviated Notation as
![\begin{displaymath}
\sigma=[a_0, a_1, a_2, a_3, \ldots].
\end{displaymath}](s1_1151.gif) |
(3) |
Bach and Shallit (1996) show how to compute the Jacobi Symbol in terms of the simple continued fraction of a
Rational Number 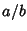 .
.
See also Continued Fraction
References
Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA:
MIT Press, pp. 343-344, 1996.
© 1996-9 Eric W. Weisstein
1999-05-26