A Sequence 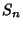 converges to the limit
converges to the limit 
if, for any 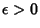 , there exists an
, there exists an  such that
such that
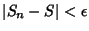 for
for 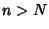 . If
. If 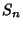 does
not converge, it is said to Diverge. Every bounded Monotonic Sequence converges.
Every unbounded Sequence diverges. This condition can also be written as
does
not converge, it is said to Diverge. Every bounded Monotonic Sequence converges.
Every unbounded Sequence diverges. This condition can also be written as
See also Conditional Convergence, Strong Convergence, Weak Convergence
© 1996-9 Eric W. Weisstein
1999-05-26
![]() converges to the limit
converges to the limit ![]()