The infinite Series
 is convergent if the Sequence of partial sums
is convergent if the Sequence of partial sums
is convergent. Conversely, a Series is divergent if the Sequence of partial sums is divergent. If  and
and 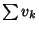 are convergent Series, then
are convergent Series, then
 and
and
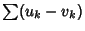 are convergent. If
are convergent. If 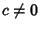 ,
then
,
then  and
and  both converge or both diverge. Convergence and divergence are unaffected by deleting a
finite number of terms from the beginning of a series. Constant terms in the denominator of a sequence can usually be
deleted without affecting convergence. All but the highest Power terms in Polynomials can
usually be deleted in both Numerator and Denominator of a Series without affecting convergence. If a
Series converges absolutely, then it converges.
both converge or both diverge. Convergence and divergence are unaffected by deleting a
finite number of terms from the beginning of a series. Constant terms in the denominator of a sequence can usually be
deleted without affecting convergence. All but the highest Power terms in Polynomials can
usually be deleted in both Numerator and Denominator of a Series without affecting convergence. If a
Series converges absolutely, then it converges.
See also Convergence Tests, Radius of Convergence
References
Bromwich, T. J. I'a. and MacRobert, T. M. An Introduction to the Theory of Infinite Series, 3rd ed. New York: Chelsea, 1991.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is convergent if the Sequence of partial sums
is convergent if the Sequence of partial sums
