|
|
|
The exponent to which a given quantity is raised is known as its Power. The expression ![]() is therefore known as
``
is therefore known as
``![]() to the
to the ![]() th Power.'' The rules for combining quantities containing powers are
called the Exponent Laws.
th Power.'' The rules for combining quantities containing powers are
called the Exponent Laws.
Special names given to various powers are listed in the following table.
| Power | Name |
| Square Root | |
| Cube Root | |
| 2 | Squared |
| 3 | Cubed |
The Sum of ![]() th Powers of the first
th Powers of the first ![]() Positive Integers
is given by Faulhaber's Formula,
Positive Integers
is given by Faulhaber's Formula,
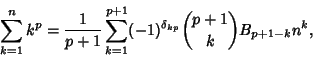
Let ![]() be the largest Integer that is not the Sum of distinct
be the largest Integer that is not the Sum of distinct ![]() th powers of Positive
Integers (Guy 1994). The first few values for
th powers of Positive
Integers (Guy 1994). The first few values for ![]() , 3, ... are 128, 12758, 5134240, 67898771,
... (Sloane's A001661).
, 3, ... are 128, 12758, 5134240, 67898771,
... (Sloane's A001661).
Catalan's Conjecture states that 8 and 9 (![]() and
and ![]() ) are the only consecutive Powers (excluding 0 and 1),
i.e., the only solution to Catalan's Diophantine Problem. This Conjecture has not yet been proved or
refuted, although R. Tijdeman has proved that there can be only a finite number of exceptions should the Conjecture
not hold. It is also known that 8 and 9 are the only consecutive Cubic and Square Numbers (in either order). Hyyrö and Makowski proved that there do not exist three
consecutive Powers (Ribenboim 1996).
) are the only consecutive Powers (excluding 0 and 1),
i.e., the only solution to Catalan's Diophantine Problem. This Conjecture has not yet been proved or
refuted, although R. Tijdeman has proved that there can be only a finite number of exceptions should the Conjecture
not hold. It is also known that 8 and 9 are the only consecutive Cubic and Square Numbers (in either order). Hyyrö and Makowski proved that there do not exist three
consecutive Powers (Ribenboim 1996).
Very few numbers of the form ![]() are Prime (where composite powers
are Prime (where composite powers ![]() need not be considered, since
need not be considered, since
![]() ). The only Prime Numbers of the form
). The only Prime Numbers of the form ![]() for
for ![]() and Prime
and Prime
![]() correspond to
correspond to ![]() , i.e.,
, i.e., ![]() ,
, ![]() ,
, ![]() , .... The only Prime Numbers of
the form
, .... The only Prime Numbers of
the form ![]() for
for ![]() and Prime
and Prime
![]() correspond to
correspond to ![]() with
with ![]() , 2, 4, 6, 10, 14, 16, 20, 24,
26, ... (Sloane's A005574).
, 2, 4, 6, 10, 14, 16, 20, 24,
26, ... (Sloane's A005574).
There are no nontrivial solutions to the equation
See also Apocalyptic Number, Biquadratic Number, Catalan's Conjecture, Catalan's Diophantine Problem, Cube Root, Cubed, Cubic Number, Exponent, Exponent Laws, Faulhaber's Formula, Figurate Number, Moessner's Theorem, Narcissistic Number, Power Rule, Square Number, Square Root, Squared, Sum, Waring's Problem
References
Barbeau, E. J. Power Play: A Country Walk through the Magical World of Numbers.
Washington, DC: Math. Assoc. Amer., 1997.
Beyer, W. H. ``Laws of Exponents.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 158, 1987.
Guy, R. K. ``Diophantine Equations.'' Ch. D in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 137, 139-198, and 153-154, 1994.
Ribenboim, P. ``Catalan's Conjecture.'' Amer. Math. Monthly 103, 529-538, 1996.
Sloane, N. J. A. Sequences
A001661/M5393
and A005574/M1010
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Spanier, J. and Oldham, K. B. ``The Integer Powers
![]() and
and ![]() '' and ``The Noninteger Powers
'' and ``The Noninteger Powers ![]() .''
Ch. 11 and 13 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 83-90 and 99-106, 1987.
.''
Ch. 11 and 13 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 83-90 and 99-106, 1987.
|
|
|
© 1996-9 Eric W. Weisstein