Series

A series is a sum of terms specified by some rule. If each term increases by a constant amount, it is said to be an Arithmetic Series. If each term equals the previous multiplied by a constant, it is said to be a Geometric Series. A series usually has an Infinite number of terms, but the phrase Infinite Series is sometimes used for emphasis or clarity.

If the sequence of partial sums comprising the first few terms of the series does not converge to a Limit (e.g., it oscillates or approaches $\pm\infty$), the series is said to diverge. An example of a convergent series is the Geometric Series

$$\sum_{n=0}^\infty ({\textstyle{1\over 2}})^n=2,$$

and an example of a divergent series is the Harmonic Series

$$\sum_{n=1}^\infty {1\over n}=\infty.$$

A number of methods known as Convergence Tests can be used to determine whether a given series converges. Although terms of a series can have either sign, convergence properties can often be computed in the ``worst case'' of all terms being Positive, and then applied to the particular series at hand. A series of terms $u_n$ is said to be Absolutely Convergent if the series formed by taking the absolute values of the $u_n$,

$$\sum_n \vert u_n\vert,$$

converges.

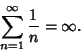
An especially strong type of convergence is called Uniform Convergence, and series which are uniformly convergent have particularly ``nice'' properties. For example, the sum of a Uniformly Convergent series of continuous functions is continuous. A Convergent Series can be Differentiated term by term, provided that the functions of the series have continuous derivatives and that the series of Derivatives is Uniformly Convergent. Finally, a Uniformly Convergent series of continuous functions can be Integrated term by term.

For a table listing the Coefficients for various series operations, see Abramowitz and Stegun (1972, p. 15).

While it can be difficult to calculate analytical expressions for arbitrary convergent infinite series, many algorithms can handle a variety of common series types. The program Mathematica ${}^{\scriptstyle\circledRsymbol}$ (Wolfram Research, Champaign, IL) implements many of these algorithms. General techniques also exist for computing the numerical values to any but the most pathological series (Braden 1992).

See also Alternating Series, Arithmetic Series, Artistic Series, Asymptotic Series, Bias (Series), Convergence Improvement, Convergence Tests, Euler-Maclaurin Integration Formulas, Geometric Series, Harmonic Series, Infinite Series, Melodic Series, q-Series, Riemann Series Theorem, Sequence, Series Expansion, Series Reversion

References

Series

Abramowitz, M. and Stegun, C. A. (Eds.). ``Infinite Series.'' §3.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.

Arfken, G. ``Infinite Series.'' Ch. 5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 277-351, 1985.

Boas, R. P. Jr. ``Partial Sums of Infinite Series, and How They Grow.'' Amer. Math. Monthly 84, 237-258, 1977.

Boas, R. P. Jr. ``Estimating Remainders.'' Math. Mag. 51, 83-89, 1978.

Borwein, J. M. and Borwein, P. B. ``Strange Series and High Precision Fraud.'' Amer. Math. Monthly 99, 622-640, 1992.

Braden, B. ``Calculating Sums of Infinite Series.'' Amer. Math. Monthly 99, 649-655, 1992.

Bromwich, T. J. I'a. and MacRobert, T. M. An Introduction to the Theory of Infinite Series, 3rd ed. New York: Chelsea, 1991.

Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.

Hardy, G. H. Divergent Series. Oxford, England: Clarendon Press, 1949.

Jolley, L. B. W. Summation of Series, 2nd rev. ed. New York: Dover, 1961.

Knopp, K. Theory and Application of Infinite Series. New York: Dover, 1990.

Mangulis, V. Handbook of Series for Scientists and Engineers. New York: Academic Press, 1965.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Series and Their Convergence.'' §5.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 159-163, 1992.

Rainville, E. D. Infinite Series. New York: Macmillan, 1967.