The improvement of the convergence properties of a Series, also called Convergence Acceleration, such
that a Series reaches its limit to within some accuracy with fewer terms than required before.
Convergence improvement can be effected by forming a linear combination with a Series whose sum is
known. Useful sums include
Kummer's transformation takes a convergent series
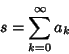 |
(5) |
and another convergent series
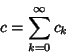 |
(6) |
with known 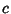 such that
such that
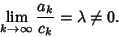 |
(7) |
Then a series with more rapid convergence to the same value is given by
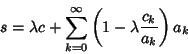 |
(8) |
(Abramowitz and Stegun 1972).
Euler's Transform takes a convergent alternating series
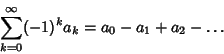 |
(9) |
into a series with more rapid convergence to the same value to
 |
(10) |
where
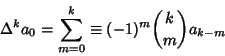 |
(11) |
(Abramowitz and Stegun 1972; Beeler et al. 1972, Item 120).
Given a series of the form
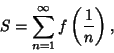 |
(12) |
where 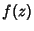 is an Analytic at 0 and on the closed unit Disk, and
is an Analytic at 0 and on the closed unit Disk, and
 |
(13) |
then the series can be rearranged to
where
 |
(15) |
is the Maclaurin Series of 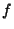 and
and 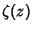 is the Riemann Zeta Function (Flajolet and Vardi 1996). The
transformed series exhibits geometric convergence. Similarly, if
is the Riemann Zeta Function (Flajolet and Vardi 1996). The
transformed series exhibits geometric convergence. Similarly, if 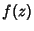 is Analytic
in
is Analytic
in  for some Positive Integer
for some Positive Integer 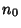 , then
, then
![\begin{displaymath}
S=\sum_{n=1}^{n_0-1}f\left({1\over n}\right)+\sum_{m=2}^\inf...
...\left[{\zeta(m)-{1\over 1^m}-\ldots-{1\over(n_0-1)^m}}\right],
\end{displaymath}](c2_1699.gif) |
(16) |
which converges geometrically (Flajolet and Vardi 1996). (16) can also be used to further accelerate the convergence of
series (14).
See also Euler's Transform, Wilf-Zeilberger Pair
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 16, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 288-289, 1985.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT
Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript. 1996.
http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps.
© 1996-9 Eric W. Weisstein
1999-05-26
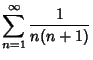

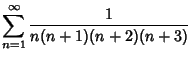
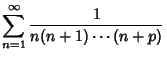
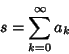
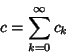
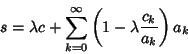
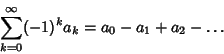

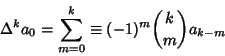
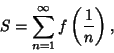
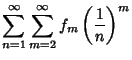
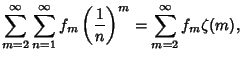

![\begin{displaymath}
S=\sum_{n=1}^{n_0-1}f\left({1\over n}\right)+\sum_{m=2}^\inf...
...\left[{\zeta(m)-{1\over 1^m}-\ldots-{1\over(n_0-1)^m}}\right],
\end{displaymath}](c2_1699.gif)