|
|
|
A Series involving coefficients of the form
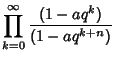 |
(1) | ||
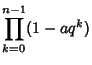 |
(2) |
| (3) | |||
| (4) |
There are a great many beautiful identities involving ![]() -series, some of which follow directly by taking the
q-Analog of standard combinatorial identities, e.g., the q-Binomial Theorem
-series, some of which follow directly by taking the
q-Analog of standard combinatorial identities, e.g., the q-Binomial Theorem
 |
(5) |
| (6) |
| (7) |
See also Borwein Conjectures, Fine's Equation, Gaussian Coefficient, Heine Hypergeometric Series, Jackson's Identity, Jacobi Identities, Mock Theta Function, q-Analog, q-Binomial Theorem, q-Cosine, q-Factorial, Q-Function, q-Gamma Function, q-Sine, Ramanujan Psi Sum, Ramanujan Theta Functions, Rogers-Ramanujan Identities
References
Andrews, G. E.
Berndt, B. C. ``
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.
Gosper, R. W. ``Experiments and Discoveries in
![]() q-Series
q-Series
![]() -Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., 1986.
-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., 1986.
![]() -Series.'' Ch. 27 in Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 261-286, 1994.
-Series.'' Ch. 27 in Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 261-286, 1994.
![]() -Trigonometry.'' Unpublished manuscript.
-Trigonometry.'' Unpublished manuscript.
|
|
|
© 1996-9 Eric W. Weisstein