|
|
|
A number often encountered when taking the ratios of distances in simple geometric figures such as the Decagon and
Dodecagon. It is denoted ![]() , or sometimes
, or sometimes ![]() (which is an abbreviation of the Greek ``tome,'' meaning ``to
cut'').
(which is an abbreviation of the Greek ``tome,'' meaning ``to
cut''). ![]() is also known as the Divine Proportion, Golden Mean, and Golden Section and is a
Pisot-Vijayaraghavan Constant. It has surprising connections with Continued
Fractions and the Euclidean Algorithm for computing the Greatest Common Divisor of two
Integers.
is also known as the Divine Proportion, Golden Mean, and Golden Section and is a
Pisot-Vijayaraghavan Constant. It has surprising connections with Continued
Fractions and the Euclidean Algorithm for computing the Greatest Common Divisor of two
Integers.
Given a Rectangle having sides in the ratio ![]() ,
, ![]() is defined such that partitioning the original
Rectangle into a Square and new Rectangle results in a new Rectangle having sides with a
ratio
is defined such that partitioning the original
Rectangle into a Square and new Rectangle results in a new Rectangle having sides with a
ratio ![]() . Such a Rectangle is called a Golden Rectangle, and successive points dividing a
Golden Rectangle into Squares lie on a Logarithmic Spiral. This figure is known as a
Whirling Square.
. Such a Rectangle is called a Golden Rectangle, and successive points dividing a
Golden Rectangle into Squares lie on a Logarithmic Spiral. This figure is known as a
Whirling Square.
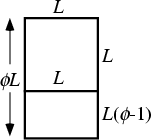
This means that
| (1) |
| (2) |
| (3) | |||
| (4) |
A geometric definition can be given in terms of the above figure. Let the ratio ![]() . The Numerator and
Denominator can then be taken as
. The Numerator and
Denominator can then be taken as
![]() and
and
![]() without loss of generality. Now define the
position of
without loss of generality. Now define the
position of ![]() by
by
| (5) |
| (6) |
| (7) |
| (8) |
![]() is the ``most'' Irrational number because it has a Continued Fraction representation
is the ``most'' Irrational number because it has a Continued Fraction representation
| (9) |
 |
(10) |
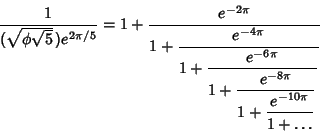 |
(11) |
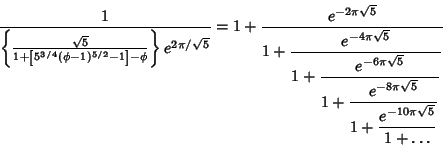 |
(12) |
The legs of a Golden Triangle are in a golden ratio to its base. In fact, this was the method used by Pythagoras
to construct ![]() . Euclid used the following construction.
. Euclid used the following construction.

Draw the Square
![]() , call
, call ![]() the Midpoint of
the Midpoint of ![]() , so that
, so that ![]() . Now draw the segment
. Now draw the segment
![]() , which has length
, which has length
| (13) |
| (14) |
The ratio of the Circumradius to the length of the side of a Decagon is also ![]() ,
,
| (15) |
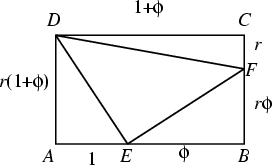
In the figure above, three Triangles can be Inscribed in the Rectangle
![]() of
arbitrary aspect ratio
of
arbitrary aspect ratio ![]() such that the three Right Triangles have equal areas by dividing
such that the three Right Triangles have equal areas by dividing ![]() and
and ![]() in the golden ratio. Then
in the golden ratio. Then
| (16) | |||
| (17) | |||
| (18) |
The golden ratio also satisfies the Recurrence Relation
| (19) |
| (20) |
| (21) |
| (22) | |||
| (23) |
For the difference equations
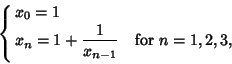 |
(24) |
| (25) |
| (26) |
The Substitution Map
| (27) | |||
| (28) |
| (29) |
| (30) |
Salem showed that the set of Pisot-Vijayaraghavan Constants is closed, with ![]() the smallest accumulation point
of the set (Le Lionnais 1983).
the smallest accumulation point
of the set (Le Lionnais 1983).
See also Beraha Constants, Decagon, Five Disks Problem, Golden Ratio Conjugate, Golden Triangle, Icosidodecahedron, Noble Number, Pentagon, Pentagram, Phi Number System, Secant Method
References
Boyer, C. B. History of Mathematics. New York: Wiley, p. 56, 1968.
Coxeter, H. S. M. ``The Golden Section, Phyllotaxis, and Wythoff's Game.'' Scripta Mathematica 19, 135-143, 1953.
Dixon, R. Mathographics. New York: Dover, pp. 30-31 and 50, 1991.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/cntfrc/cntfrc.html
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/gold/gold.html
Gardner, M. ``Phi: The Golden Ratio.'' Ch. 8 in
The Second Scientific American Book of Mathematical Puzzles & Diversions, A New Selection.
New York: Simon and Schuster, 1961.
Gardner, M. ``Notes on a Fringe-Watcher: The Cult of the Golden Ratio.'' Skeptical Inquirer 18, 243-247, 1994.
Herz-Fischler, R. A Mathematical History of the Golden Number. New York: Dover, 1998.
Huntley, H. E. The Divine Proportion. New York: Dover, 1970.
Knott, R. ``Fibonacci Numbers and the Golden Section.''
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 40, 1983.
Markowsky, G. ``Misconceptions About the Golden Ratio.'' College Math. J. 23, 2-19, 1992.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 122-134, 1990.
Pappas, T. ``Anatomy & the Golden Section.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra,
pp. 32-33, 1989.
Ramanathan, K. G. ``On Ramanujan's Continued Fraction.'' Acta. Arith. 43, 209-226, 1984.
Sloane, N. J. A. Sequences
A003849,
A000012/M0003,
A000201/M2322,
A001622/M4046,
A001950/M1332
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() Golden Ratio
Golden Ratio
|
|
|
© 1996-9 Eric W. Weisstein