|
|
|
The sequence of numbers defined by the ![]() in the Lucas Sequence. They are companions to the Lucas
Numbers and satisfy the same Recurrence Relation,
in the Lucas Sequence. They are companions to the Lucas
Numbers and satisfy the same Recurrence Relation,
| (1) |
The ratios of alternate Fibonacci numbers are given by the convergents to ![]() , where
, where ![]() is the Golden Ratio,
and are said to measure the fraction of a turn between successive leaves on the stalk of a plant (Phyllotaxis): 1/2 for
elm and linden, 1/3 for beech and hazel, 2/5 for oak and apple, 3/8 for poplar and rose, 5/13 for willow and almond,
etc. (Coxeter 1969, Ball and Coxeter 1987). The Fibonacci numbers are sometimes called Pine Cone Numbers
(Pappas 1989, p. 224).
is the Golden Ratio,
and are said to measure the fraction of a turn between successive leaves on the stalk of a plant (Phyllotaxis): 1/2 for
elm and linden, 1/3 for beech and hazel, 2/5 for oak and apple, 3/8 for poplar and rose, 5/13 for willow and almond,
etc. (Coxeter 1969, Ball and Coxeter 1987). The Fibonacci numbers are sometimes called Pine Cone Numbers
(Pappas 1989, p. 224).
Another Recurrence Relation for the Fibonacci numbers is
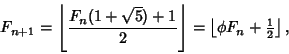 |
(2) |
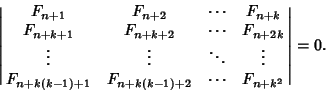 |
(3) |
The Generating Function for the Fibonacci numbers is
 |
(4) |
Yuri Matijasevic (1970) proved that the equation ![]() is a Diophantine Equation. This led to the proof of
the impossibility of the tenth of Hilbert's Problems (does there
exist a general method for solving Diophantine Equations?) by Julia
Robinson and Martin Davis in 1970.
is a Diophantine Equation. This led to the proof of
the impossibility of the tenth of Hilbert's Problems (does there
exist a general method for solving Diophantine Equations?) by Julia
Robinson and Martin Davis in 1970.
The Fibonacci number ![]() gives the number of ways for
gives the number of ways for ![]() Dominoes to cover a
Dominoes to cover a ![]() Checkerboard, as illustrated in the following diagrams (Dickau).
Checkerboard, as illustrated in the following diagrams (Dickau).



The number of ways of picking a Set (including the Empty Set) from the numbers 1, 2, ..., ![]() without
picking two consecutive numbers is
without
picking two consecutive numbers is ![]() . The number of ways of picking a set (including the Empty Set) from
the numbers 1, 2, ...,
. The number of ways of picking a set (including the Empty Set) from
the numbers 1, 2, ..., ![]() without picking two consecutive numbers (where 1 and
without picking two consecutive numbers (where 1 and ![]() are now consecutive) is
are now consecutive) is
![]() , where
, where ![]() is a Lucas Number. The probability of not getting two heads in a row in
is a Lucas Number. The probability of not getting two heads in a row in ![]() tosses of a Coin is
tosses of a Coin is ![]() (Honsberger 1985, pp. 120-122). Fibonacci numbers are also
related to the number of ways in which
(Honsberger 1985, pp. 120-122). Fibonacci numbers are also
related to the number of ways in which ![]() Coin Tosses can be made such that there are not three
consecutive heads or tails. The number of ideals of an
Coin Tosses can be made such that there are not three
consecutive heads or tails. The number of ideals of an ![]() -element Fence Poset is the Fibonacci number
-element Fence Poset is the Fibonacci number ![]() .
.
Sum identities are
 |
(5) |
| (6) |
| (7) |
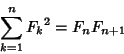 |
(8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
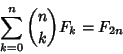 |
(22) |
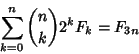 |
(23) |
In terms of the Lucas Number ![]() ,
,
| (24) |
| (25) |
| (26) |
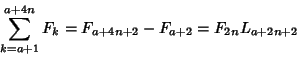 |
(27) |
| (28) |
| (29) |
| (30) |
| (31) |
The equation (1) is a Linear Recurrence Sequence
| (32) |
| (33) |
| (34) |
| (35) |
| (36) |
![\begin{displaymath}
F_n = \left[{{1\over\sqrt{5}}\left({1+\sqrt{5}\over 2}\right)^n}\right]=\left[{\phi^n\over\sqrt{5}}\right],
\end{displaymath}](f_828.gif) |
(37) |
From (1), the Ratio of consecutive terms is
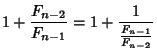 |
|||
![$\displaystyle 1+{1\over {\strut 1+{\strut 1\over \strut {F_{n-3}\over F_{n-2}}}}} = \left[{1, 1, \ldots, {F_{2}\over F_1}}\right]$](f_832.gif) |
|||
![$\displaystyle [\underbrace{1, 1, \ldots, 1}_{n-1}],$](f_833.gif) |
(38) |
| (39) |
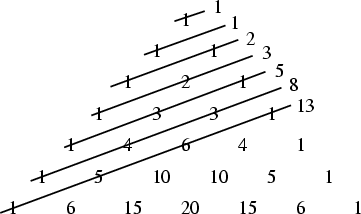
The ``Shallow Diagonals'' of Pascal's Triangle sum to Fibonacci numbers (Pappas 1989),
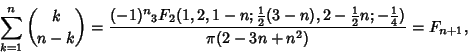 |
(40) |
where
![]() is a Generalized Hypergeometric Function.
is a Generalized Hypergeometric Function.
The sequence of final digits in Fibonacci numbers repeats in cycles of 60. The last two digits repeat in 300, the last
three in 1500, the last four in 15,000, etc.
 |
(41) |
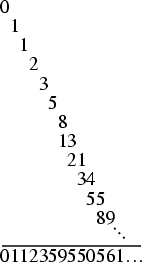
which is equal to the fractional digits of ![]() ,
,
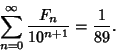 |
(42) |
For ![]() ,
, ![]() Iff
Iff ![]() .
. ![]() Iff
Iff ![]() divides into
divides into ![]() an Even number of times.
an Even number of times.
![]() (Michael 1964; Honsberger 1985, pp. 131-132). No Odd Fibonacci number is divisible by 17 (Honsberger 1985,
pp. 132 and 242). No Fibonacci number
(Michael 1964; Honsberger 1985, pp. 131-132). No Odd Fibonacci number is divisible by 17 (Honsberger 1985,
pp. 132 and 242). No Fibonacci number ![]() is ever of the form
is ever of the form ![]() or
or ![]() where
where ![]() is a Prime number (Honsberger 1985,
p. 133).
is a Prime number (Honsberger 1985,
p. 133).
Consider the sum
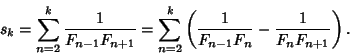 |
(43) |
| (44) |
| (45) |
 |
(46) |
| (47) | |||
| (48) |
| (49) |
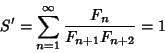 |
(50) |
 |
(51) |
The Fibonacci numbers are Complete. In fact, dropping one number still leaves a Complete
Sequence, although dropping two numbers does not (Honsberger 1985, pp. 123 and 126). Dropping two terms from the Fibonacci
numbers produces a sequence which is not even Weakly Complete (Honsberger 1985, p. 128).
However, the sequence
| (52) |
For a discussion of Square Fibonacci numbers, see Cohn (1964), who proved that the only
Square Number Fibonacci numbers are 1 and ![]() (Cohn 1964, Guy 1994). Ming (1989) proved that the only
Triangular Fibonacci numbers are 1, 3, 21, and 55. The Fibonacci and Lucas
Numbers have no common terms except 1 and 3. The only Cubic Fibonacci numbers are 1 and 8.
(Cohn 1964, Guy 1994). Ming (1989) proved that the only
Triangular Fibonacci numbers are 1, 3, 21, and 55. The Fibonacci and Lucas
Numbers have no common terms except 1 and 3. The only Cubic Fibonacci numbers are 1 and 8.
| (53) |
| (54) |
In 1975, James P. Jones showed that the Fibonacci numbers are the Positive Integer values of the Polynomial
| (55) |
Every ![]() that is Prime has a Prime index
that is Prime has a Prime index ![]() , with the exception of
, with the exception of ![]() . However, the converse is not true
(i.e., not every prime index
. However, the converse is not true
(i.e., not every prime index ![]() gives a Prime
gives a Prime ![]() ). The first few Prime Fibonacci numbers are for
). The first few Prime Fibonacci numbers are for ![]() , 4, 5, 7,
11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571, ... (Sloane's A001605; Dubner and Keller 1999).
Gardner's statement that
, 4, 5, 7,
11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571, ... (Sloane's A001605; Dubner and Keller 1999).
Gardner's statement that ![]() is prime is incorrect, especially since 531 is not even Prime (Gardner 1979, p. 161).
It is not known if there are an Infinite number of Fibonacci primes.
is prime is incorrect, especially since 531 is not even Prime (Gardner 1979, p. 161).
It is not known if there are an Infinite number of Fibonacci primes.
The Fibonacci numbers ![]() , are Squareful for
, are Squareful for ![]() , 12, 18, 24, 25, 30, 36, 42, 48, 50, 54, 56, 60, 66, ...,
372, 375, 378, 384, ... (Sloane's A037917) and Squarefree for
, 12, 18, 24, 25, 30, 36, 42, 48, 50, 54, 56, 60, 66, ...,
372, 375, 378, 384, ... (Sloane's A037917) and Squarefree for ![]() , 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, ...
(Sloane's A037918).
, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, ...
(Sloane's A037918). ![]() and
and ![]() for all
for all ![]() , but no Squareful Fibonacci numbers
, but no Squareful Fibonacci numbers ![]() are known with
are known with ![]() Prime.
Prime.
See also Cassini's Identity, Fast Fibonacci Transform, Fibonacci Dual Theorem, Fibonacci n-Step Number, Fibonacci Q-Matrix, Generalized Fibonacci Number, Inverse Tangent, Linear Recurrence Sequence, Lucas Sequence, Near Noble Number, Pell Sequence, Rabbit Constant, Stolarsky Array, Tetranacci Number, Tribonacci Number, Wythoff Array, Zeckendorf Representation, Zeckendorf's Theorem
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 56-57, 1987.
Basin, S. L. and Hoggatt, V. E. Jr. ``A Primer on the Fibonacci Sequence.'' Fib. Quart. 1, 1963.
Basin, S. L. and Hoggatt, V. E. Jr. ``A Primer on the Fibonacci Sequence--Part II.'' Fib. Quart. 1, 61-68, 1963.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 94-101, 1987.
Brillhart, J.; Montgomery, P. L.; and Silverman, R. D. ``Tables of Fibonacci and Lucas Factorizations.''
Math. Comput. 50, 251-260 and S1-S15, 1988.
Brook, M. ``Fibonacci Formulas.'' Fib. Quart. 1, 60, 1963.
Brousseau, A. ``Fibonacci Numbers and Geometry.'' Fib. Quart. 10, 303-318, 1972.
Clark, D. Solution to Problem 10262. Amer. Math. Monthly 102, 467, 1995.
Cohn, J. H. E. ``On Square Fibonacci Numbers.'' J. London Math. Soc. 39, 537-541, 1964.
Conway, J. H. and Guy, R. K. ``Fibonacci Numbers.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 111-113, 1996.
Coxeter, H. S. M. ``The Golden Section and Phyllotaxis.'' Ch. 11 in Introduction to Geometry, 2nd ed.
New York: Wiley, 1969.
Dickau, R. M. ``Fibonacci Numbers.''
http://www.prairienet.org/~pops/fibboard.html.
Dubner, H. and Keller, W. ``New Fibonacci and Lucas Primes.'' Math. Comput. 68, 417-427 and S1-S12, 1999.
Freitag, H. Solution to Problem B-772. ``An Integral Ratio.'' Fib. Quart. 34, 82, 1996.
Gardner, M.
Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American.
New York: Knopf, 1979.
Graham, R. ``A Property of Fibonacci Numbers.'' Fib. Quart. 2, 1-10, 1964.
Guy, R. K. ``Fibonacci Numbers of Various Shapes.'' §D26 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 194-195, 1994.
Halton, J. H. ``On a General Fibonacci Identity.'' Fib. Quart. 3, 31-43, 1965.
Hoggatt, V. E. Jr. The Fibonacci and Lucas Numbers. Boston, MA: Houghton Mifflin, 1969.
Hoggatt, V. E. Jr. and Ruggles, I. D. ``A Primer on the Fibonacci Sequence--Part III.'' Fib. Quart. 1, 61-65, 1963.
Hoggatt, V. E. Jr. and Ruggles, I. D. ``A Primer on the Fibonacci Sequence--Part IV.'' Fib. Quart. 1, 65-71, 1963.
Hoggatt, V. E. Jr. and Ruggles, I. D. ``A Primer on the Fibonacci Sequence--Part V.'' Fib. Quart. 2, 59-66, 1964.
Hoggatt, V. E. Jr.; Cox, N.; and Bicknell, M. ``A Primer for the Fibonacci Numbers: Part XII.'' Fib. Quart. 11, 317-331, 1973.
Honsberger, R. ``A Second Look at the Fibonacci and Lucas Numbers.'' Ch. 8 in Mathematical Gems III.
Washington, DC: Math. Assoc. Amer., 1985.
Knott, R. ``Fibonacci Numbers and the Golden Section.''
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 146, 1983.
Leyland, P. ftp://sable.ox.ac.uk/pub/math/factors/fibonacci.Z.
Matijasevic, Yu. V. ``Solution to of the Tenth Problem of Hilbert.'' Mat. Lapok 21, 83-87, 1970.
Matijasevich, Yu. V. Hilbert's Tenth Problem. Cambridge, MA: MIT Press, 1993.
Michael, G. ``A New Proof for an Old Property.'' Fib. Quart. 2, 57-58, 1964.
Ming, L. ``On Triangular Fibonacci Numbers.'' Fib. Quart. 27, 98-108, 1989.
Ogilvy, C. S. and Anderson, J. T. ``Fibonacci Numbers.'' Ch. 11 in Excursions in Number Theory. New York: Dover,
pp. 133-144, 1988.
Pappas, T. ``Fibonacci Sequence,'' ``Pascal's Triangle, the Fibonacci Sequence & Binomial Formula,'' ``The Fibonacci Trick,'' and
``The Fibonacci Sequence & Nature.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 28-29, 40-41, 51, 106, and 222-225, 1989.
Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, pp. 49-57, 1991.
Sloane, N. J. A.
A037917,
A037918
A000045/M0692, and
A001605/M2309
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Vorob'ev, N. N. Fibonacci Numbers. New York: Blaisdell, 1961.
![]() Fibonacci Numbers
Fibonacci Numbers
|
|
|
© 1996-9 Eric W. Weisstein