|
|
|
The numbers produced by the ![]() recurrence in the Lucas Sequence with
recurrence in the Lucas Sequence with ![]() are called Lucas numbers. They
are the companions to the Fibonacci Numbers
are called Lucas numbers. They
are the companions to the Fibonacci Numbers ![]() and satisfy the same recurrence
and satisfy the same recurrence
| (1) |
In terms of the Fibonacci Numbers,
| (2) |
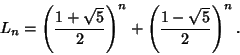 |
(3) |
| (4) |
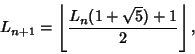 |
(5) |
| (6) |
 |
(7) |
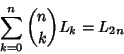 |
(8) |
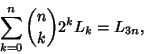 |
(9) |
![]() (
(![]() Divides
Divides ![]() ) Iff
) Iff ![]() Divides into
Divides into ![]() an Even number of times.
an Even number of times.
![]() Iff
Iff ![]() divides into
divides into ![]() an Odd number of times.
an Odd number of times. ![]() always ends in 2 (Honsberger 1985, p. 137).
always ends in 2 (Honsberger 1985, p. 137).
Defining
 |
(10) |
| (11) |
The number of ways of picking a set (including the Empty Set) from the numbers 1, 2, ..., ![]() without picking
two consecutive numbers (where 1 and
without picking
two consecutive numbers (where 1 and ![]() are now consecutive) is
are now consecutive) is
![]() (Honsberger 1985, p. 122).
(Honsberger 1985, p. 122).
The only Square Numbers in the Lucas sequence are 1 and 4, as proved by John H. E. Cohn (Alfred 1964).
The only Triangular Lucas numbers are 1, 3, and 5778 (Ming 1991). The only Lucas Cubic
Number is 1. The first few Lucas Primes ![]() occur for
occur for ![]() , 4, 5, 7, 8, 11, 13, 16, 17, 19, 31, 37, 41, 47, 53, 61, 71,
79, 113, 313, 353, ... (Dubner and Keller 1999, Sloane's A001606).
, 4, 5, 7, 8, 11, 13, 16, 17, 19, 31, 37, 41, 47, 53, 61, 71,
79, 113, 313, 353, ... (Dubner and Keller 1999, Sloane's A001606).
See also Fibonacci Number
References
Alfred, Brother U. ``On Square Lucas Numbers.'' Fib. Quart. 2, 11-12, 1964.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 94-101, 1987.
Brillhart, J.; Montgomery, P. L.; and Solverman, R. D. ``Tables of Fibonacci and Lucas Factorizations.''
Math. Comput. 50, 251-260 and S1-S15, 1988.
Brown, J. L. Jr. ``Unique Representation of Integers as Sums of Distinct Lucas Numbers.'' Fib. Quart. 7, 243-252, 1969.
Dubner, H. and Keller, W. ``New Fibonacci and Lucas Primes.'' Math. Comput. 68, 417-427 and S1-S12, 1999.
Guy, R. K. ``Fibonacci Numbers of Various Shapes.'' §D26 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 194-195, 1994.
Hoggatt, V. E. Jr. The Fibonacci and Lucas Numbers. Boston, MA: Houghton Mifflin, 1969.
Honsberger, R. ``A Second Look at the Fibonacci and Lucas Numbers.'' Ch. 8 in Mathematical Gems III.
Washington, DC: Math. Assoc. Amer., 1985.
Leyland, P. ftp://sable.ox.ac.uk/pub/math/factors/lucas.Z.
Ming, L. ``On Triangular Lucas Numbers.'' Applications of Fibonacci Numbers, Vol. 4
(Ed. G. E. Bergum, A. N. Philippou, and A. F. Horadam). Dordrecht, Netherlands: Kluwer, pp. 231-240, 1991.
Sloane, N. J. A. Sequences
A000204/M2341
and A001606/M0961
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein