|
|
|
The generalized hypergeometric function is given by a Hypergeometric Series, i.e., a series for which the ratio of
successive terms can be written
| (1) |
![$\displaystyle {}_pF_q\left[{\begin{array}{c}a_1, a_2, \cdots, a_p\\ b_1, b_2, \cdots, b_q\end{array}; x}\right]$](g_1187.gif) |
(2) | ||
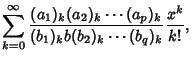 |
(3) |
| (4) |
| (5) |
![]() is ``the'' Hypergeometric Function, and
is ``the'' Hypergeometric Function, and
![]() is the Confluent
Hypergeometric Function. A function of the form
is the Confluent
Hypergeometric Function. A function of the form ![]() is called a Confluent Hypergeometric Limit Function.
is called a Confluent Hypergeometric Limit Function.
The generalized hypergeometric function
| (6) |
| (7) |
| (8) |
![\begin{displaymath}
z^{1-b_1}{}_{p+1}F_p\left[{\matrix{
1+a_1-b_1, 1-a_2-b_2,\hf...
... 1-b_2-b_1, \ldots,\hfill\cr
\hfill 1-b_p-b_1\cr} ; z}\right].
\end{displaymath}](g_1199.gif) |
(9) |
A generalized hypergeometric equation is termed ``well posed'' if
| (10) |
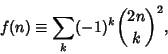 |
(11) |
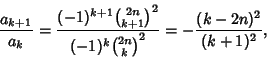 |
(12) |
| (13) |
Gosper (1978) discovered a slew of unusual hypergeometric function identities, many of which were subsequently proven by Gessel and Stanton (1982). An important generalization of Gosper's technique, called Zeilberger's Algorithm, in turn led to the powerful machinery of the Wilf-Zeilberger Pair (Zeilberger 1990).
Special hypergeometric identities include Gauss's Hypergeometric Theorem
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
Gessel (1994) found a slew of new identities using Wilf-Zeilberger Pairs, including the following:
| (20) |
| (21) |
| (22) |
| (23) |
See also Carlson's Theorem, Clausen Formula, Confluent Hypergeometric Function, Confluent Hypergeometric Limit Function, Dixon's Theorem, Dougall-Ramanujan Identity, Dougall's Theorem, Gosper's Algorithm, Heine Hypergeometric Series, Hypergeometric Function, Hypergeometric Identity, Hypergeometric Series, Jackson's Identity, Kummer's Theorem, Ramanujan's Hypergeometric Identity, Saalschütz's Theorem, Saalschützian, Sister Celine's Method, Thomae's Theorem, Watson's Theorem, Whipple's Transformation, Wilf-Zeilberger Pair, Zeilberger's Algorithm
References
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.
Dwork, B. Generalized Hypergeometric Functions. Oxford, England: Clarendon Press, 1990.
Exton, H. Multiple Hypergeometric Functions and Applications. New York: Wiley, 1976.
Gessel, I. ``Finding Identities with the WZ Method.'' Theoret. Comput. Sci. To appear.
Gessel, I. and Stanton, D. ``Strange Evaluations of Hypergeometric Series.'' SIAM J. Math. Anal. 13, 295-308, 1982.
Gosper, R. W. ``Decision Procedures for Indefinite Hypergeometric Summation.'' Proc. Nat. Acad. Sci. USA 75, 40-42, 1978.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, 1996.
Saxena, R. K. and Mathai, A. M. Generalized Hypergeometric Functions with Applications in Statistics and Physical Sciences.
New York: Springer-Verlag, 1973.
Slater, L. J. Generalized Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1966.
Zeilberger, D. ``A Fast Algorithm for Proving Terminating Hypergeometric Series Identities.'' Discrete Math. 80, 207-211, 1990.
|
|
|
© 1996-9 Eric W. Weisstein