Sister Celine's Method

A method for finding Recurrence Relations for hypergeometric polynomials directly from the series expansions of the polynomials. The method is effective and easily implemented, but usually slower than Zeilberger's Algorithm. Given a sum $f(n)=\sum_k F(n,k)$, the method operates by finding a recurrence of the form

$$\sum_{i=0}^I \sum_{j=0}^J a_{ij}(n)F(n-j,k-i)=0$$

by proceeding as follows (Petkovsek et al. 1996, p. 59):

1. Fix trial values of $I$ and $J$.

2. Assume a recurrence formula of the above form where $a_{ij}(n)$ are to be solved for.

3. Divide each term of the assumed recurrence by $F(n,k)$ and reduce every ratio $F(n-j,k-i)/F(n,k)$ by simplifying the ratios of its constituent factorials so that only Rational Functions in $n$ and $k$ remain.

4. Put the resulting expression over a common Denominator, then collect the numerator as a Polynomial in $k$.

5. Solve the system of linear equations that results after setting the coefficients of each power of $k$ in the Numerator to 0 for the unknown coefficients $a_{ij}$.

6. If no solution results, start again with larger $I$ or $J$.

Under suitable hypotheses, a ``fundamental theorem'' (Verbaten 1974, Wilf and Zeilberger 1992, Petkovsek et al. 1996) guarantees that this algorithm always succeeds for large enough $I$ and $J$ (which can be estimated in advance). The theorem also generalizes to multivariate sums and to $q$- and multi-$q$-sums (Wilf and Zeilberger 1992, Petkovsek et al. 1996).

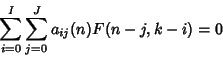
See also Generalized Hypergeometric Function, Gosper's Algorithm, Hypergeometric Identity, Hypergeometric Series, Zeilberger's Algorithm

References

Fasenmyer, Sister M. C. Some Generalized Hypergeometric Polynomials. Ph.D. thesis. University of Michigan, Nov. 1945.

Fasenmyer, Sister M. C. ``Some Generalized Hypergeometric Polynomials.'' Bull. Amer. Math. Soc. 53, 806-812, 1947.

Fasenmyer, Sister M. C. ``A Note on Pure Recurrence Relations.'' Amer. Math. Monthly 56, 14-17, 1949.

Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. ``Sister Celine's Method.'' Ch. 4 in A=B. Wellesley, MA: A. K. Peters, pp. 55-72, 1996.

Rainville, E. D. Chs. 14 and 18 in Special Functions. New York: Chelsea, 1971.

Verbaten, P. ``The Automatic Construction of Pure Recurrence Relations.'' Proc. EUROSAM '74, ACM-SIGSAM Bull. 8, 96-98, 1974.

Wilf, H. S. and Zeilberger, D. ``An Algorithmic Proof Theory for Hypergeometric (Ordinary and ``$q$'') Multisum/Integral Identities.'' Invent. Math. 108, 575-633, 1992.