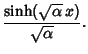In 1757, V. Riccati first recorded the generalizations of the Hyperbolic Functions defined by
 |
(1) |
for  , ...,
, ..., 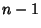 , where
, where 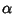 is Complex, with the value at
is Complex, with the value at  defined by
defined by
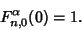 |
(2) |
This is called the 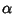 -hyperbolic function of order
-hyperbolic function of order  of the
of the 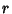 th kind. The functions
th kind. The functions
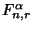 satisfy
satisfy
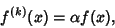 |
(3) |
where
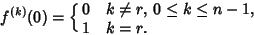 |
(4) |
In addition,
 |
(5) |
The functions give a generalized Euler Formula
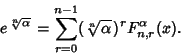 |
(6) |
Since there are 
 th roots of
th roots of 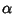 , this gives a system of
, this gives a system of  linear equations. Solving for
linear equations. Solving for
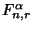 gives
gives
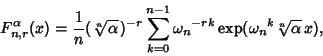 |
(7) |
where
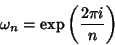 |
(8) |
is a Primitive Root of Unity.
The Laplace Transform is
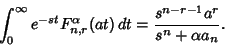 |
(9) |
The generalized hyperbolic function is also related to the Mittag-Leffler Function 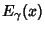 by
by
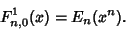 |
(10) |
The values 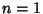 and
and 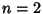 give the exponential and circular/hyperbolic functions (depending on the sign of
give the exponential and circular/hyperbolic functions (depending on the sign of 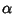 ),
respectively.
),
respectively.
For 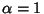 , the first few functions are
, the first few functions are
See also Hyperbolic Functions, Mittag-Leffler Function
References
Kaufman, H. ``A Biographical Note on the Higher Sine Functions.'' Scripta Math. 28, 29-36, 1967.
Muldoon, M. E. and Ungar, A. A. ``Beyond Sin and Cos.'' Math. Mag. 69, 3-14, 1996.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, 1996.
Ungar, A. ``Generalized Hyperbolic Functions.'' Amer. Math. Monthly 89, 688-691, 1982.
Ungar, A. ``Higher Order Alpha-Hyperbolic Functions.'' Indian J. Pure. Appl. Math. 15, 301-304, 1984.
© 1996-9 Eric W. Weisstein
1999-05-25

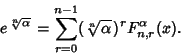
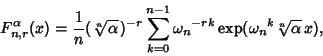
![]() and
and ![]() give the exponential and circular/hyperbolic functions (depending on the sign of
give the exponential and circular/hyperbolic functions (depending on the sign of ![]() ),
respectively.
),
respectively.