|
|
|
The Laplace transform is an Integral Transform perhaps second only to the Fourier Transform in its utility in solving physical problems. Due to its useful properties, the Laplace transform is particularly useful in solving linear Ordinary Differential Equations such as those arising in the analysis of electronic circuits.
The (one-sided) Laplace transform ![]() (not to be confused with the Lie Derivative) is defined by
(not to be confused with the Lie Derivative) is defined by
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
The Laplace transform is Linear since
|
|
|
|
|
|
|
|
(7) |
|
|
Range | |
| 1 | ||
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
In the above table, ![]() is the zeroth order Bessel Function of the First Kind,
is the zeroth order Bessel Function of the First Kind, ![]() is the Delta
Function, and
is the Delta
Function, and ![]() is the Heaviside Step Function. The Laplace transform has many important properties.
is the Heaviside Step Function. The Laplace transform has many important properties.
The Laplace transform of a Convolution is given by
| (8) |
| (9) |
Now consider Differentiation. Let ![]() be continuously differentiable
be continuously differentiable ![]() times in
times in ![]() . If
. If
![]() , then
, then
| (10) |
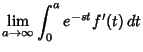 |
|||
![$\displaystyle \lim_{a\to\infty}\left[{e^{-st}f(t)]^a_0 + s \int^a_0 e^{-st}f(t)\,dt}\right]$](l1_725.gif) |
|||
![$\displaystyle \lim_{a\to\infty}\left[{e^{-sa}f(a)-f(0)+s\int^a_0 e^{-st}f(t)\,dt}\right]$](l1_726.gif) |
|||
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Consider Exponentiation. If
![]() for
for ![]() , then
, then
![]() for
for ![]() .
.
![$\displaystyle \int^\infty_0 f(t)e^{-(s-a)t}\,dt = \int^\infty_0 [f(t)e^{at}]e^{-st}\,dt$](l1_738.gif) |
|||
| (17) |
Consider Integration. If ![]() is piecewise continuous and
is piecewise continuous and
![]() , then
, then
| (18) |
The inverse transform is known as the Bromwich Integral, or sometimes the Fourier-Mellin Integral.
See also Bromwich Integral, Fourier-Mellin Integral, Fourier Transform, Integral Transform, Laplace-Stieltjes Transform, Operational Mathematics
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Laplace Transforms.'' Ch. 29 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 1019-1030, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 824-863, 1985.
Churchill, R. V. Operational Mathematics. New York: McGraw-Hill, 1958.
Doetsch, G. Introduction to the Theory and Application of the Laplace Transformation. Berlin: Springer-Verlag, 1974.
Franklin, P. An Introduction to Fourier Methods and the Laplace Transformation. New York: Dover, 1958.
Jaeger, J. C. and Newstead, G. H. An Introduction to the Laplace Transformation with Engineering Applications.
London: Methuen, 1949.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 467-469, 1953.
Spiegel, M. R. Theory and Problems of Laplace Transforms. New York: McGraw-Hill, 1965.
Widder, D. V. The Laplace Transform. Princeton, NJ: Princeton University Press, 1941.
![]() Laplace Transforms
Laplace Transforms
|
|
|
© 1996-9 Eric W. Weisstein