A convolution is an integral which expresses the amount of overlap of one function 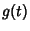 as it is shifted over another
function
as it is shifted over another
function 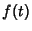 . It therefore ``blends'' one function with another. For example, in
synthesis imaging,
. It therefore ``blends'' one function with another. For example, in
synthesis imaging,  the measured Dirty Map is a convolution of the ``true'' CLEAN Map with the
Dirty Beam (the Fourier Transform of the sampling distribution). The convolution is sometimes also known by
its German name, Faltung (``folding''). A convolution over a finite range
the measured Dirty Map is a convolution of the ``true'' CLEAN Map with the
Dirty Beam (the Fourier Transform of the sampling distribution). The convolution is sometimes also known by
its German name, Faltung (``folding''). A convolution over a finite range ![$[0, t]$](c3_28.gif) is given
by
is given
by
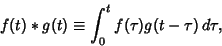 |
(1) |
where the symbol 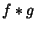 (occasionally also written as
(occasionally also written as 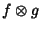 ) denotes convolution of
) denotes convolution of 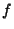 and
and 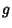 . Convolution is more
often taken over an infinite range,
. Convolution is more
often taken over an infinite range,
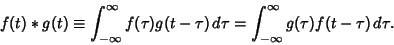 |
(2) |
Let 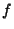 ,
, 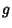 , and
, and 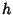 be arbitrary functions and
be arbitrary functions and  a constant. Convolution has the following properties:
a constant. Convolution has the following properties:
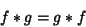 |
(3) |
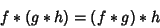 |
(4) |
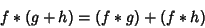 |
(5) |
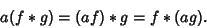 |
(6) |
The Integral identity
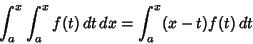 |
(7) |
also gives a convolution. Taking the Derivative of a convolution gives
 |
(8) |
The Area under a convolution is the product of areas under the factors,
The horizontal Centroids add
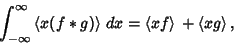 |
(10) |
as do the Variances
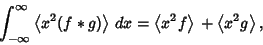 |
(11) |
where
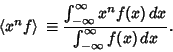 |
(12) |
See also Autocorrelation, Convolution Theorem, Cross-Correlation,
Wiener-Khintchine Theorem
References
 Convolution
Convolution
Bracewell, R. ``Convolution.'' Ch. 3 in The Fourier Transform and Its Applications.
New York: McGraw-Hill, pp. 25-50, 1965.
Hirschman, I. I. and Widder, D. V. The Convolution Transform. Princeton, NJ: Princeton University Press, 1955.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 464-465, 1953.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Convolution and Deconvolution Using the FFT.'' §13.1 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 531-537, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() as it is shifted over another
function
as it is shifted over another
function ![]() . It therefore ``blends'' one function with another. For example, in
synthesis imaging,
. It therefore ``blends'' one function with another. For example, in
synthesis imaging, ![]() the measured Dirty Map is a convolution of the ``true'' CLEAN Map with the
Dirty Beam (the Fourier Transform of the sampling distribution). The convolution is sometimes also known by
its German name, Faltung (``folding''). A convolution over a finite range
the measured Dirty Map is a convolution of the ``true'' CLEAN Map with the
Dirty Beam (the Fourier Transform of the sampling distribution). The convolution is sometimes also known by
its German name, Faltung (``folding''). A convolution over a finite range ![]() is given
by
is given
by
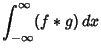
![$\displaystyle \int_{-\infty}^\infty\left[{\int_{-\infty}^\infty f(u)g(x-u)\,du}\right]\,dx$](c3_44.gif)
![$\displaystyle \int_{-\infty}^\infty f(u)\left[{\int_{-\infty}^\infty g(x-u)\,dx}\right]\,du$](c3_45.gif)
![$\displaystyle \left[{\int_{-\infty}^\infty f(u)\,du}\right]\left[{\int_{-\infty}^\infty g(x)\,dx}\right].$](c3_46.gif)
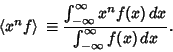
![]() Convolution
Convolution