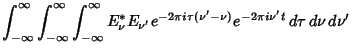Recall the definition of the Autocorrelation function  of a function
of a function  ,
,
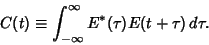 |
(1) |
Also recall that the Fourier Transform of  is defined by
is defined by
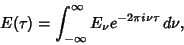 |
(2) |
giving a Complex Conjugate of
 |
(3) |
Plugging 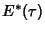 and
and  into the Autocorrelation function therefore gives
into the Autocorrelation function therefore gives
so, amazingly, the Autocorrelation is simply given by the Fourier Transform of the Absolute Square
of  ,
,
![\begin{displaymath}
C(t) = {\mathcal F}[\vert E(\nu)\vert^2].
\end{displaymath}](w_902.gif) |
(5) |
The Wiener-Khintchine theorem is a special case of the Cross-Correlation Theorem with 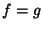 .
.
See also Autocorrelation, Cross-Correlation Theorem, Fourier Transform
© 1996-9 Eric W. Weisstein
1999-05-26
![]() of a function
of a function ![]() ,
,
![$\displaystyle \int_{-\infty}^\infty \left[{\int_{-\infty}^\infty E_\nu^* e^{2\p...
...[{\int_{-\infty}^\infty E_{\nu'} e^{-2\pi i\nu'(t+\tau)}\, d\nu'}\right]\,d\tau$](w_895.gif)