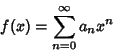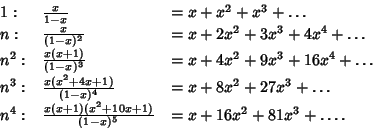A Power Series
whose Coefficients give the Sequence 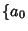 ,
, 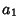 , ...
, ... .
The Mathematica
.
The Mathematica
 (Wolfram Research, Champaign, IL) function DiscreteMath`RSolve`PowerSum
gives the generating function of a given expression, and ExponentialPowerSum gives the exponential generating function.
(Wolfram Research, Champaign, IL) function DiscreteMath`RSolve`PowerSum
gives the generating function of a given expression, and ExponentialPowerSum gives the exponential generating function.
Generating functions for the first few powers are
See also Moment-Generating Function, Recurrence Relation
References
Wilf, H. S. Generatingfunctionology, 2nd ed. New York: Academic Press, 1990.
© 1996-9 Eric W. Weisstein
1999-05-25