|
|
|
The ![]() Polynomials obtained by setting
Polynomials obtained by setting ![]() and
and ![]() in the Lucas Polynomial
Sequence. (The corresponding
in the Lucas Polynomial
Sequence. (The corresponding ![]() Polynomials are called Lucas
Polynomials.) The Fibonacci polynomials are defined by the Recurrence Relation
Polynomials are called Lucas
Polynomials.) The Fibonacci polynomials are defined by the Recurrence Relation
| (1) |
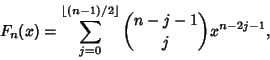 |
(2) |
| (3) |
The Fibonacci polynomials are related to the Morgan-Voyce Polynomials by
| (4) | |||
| (5) |
See also Brahmagupta Polynomial, Fibonacci Number, Morgan-Voyce Polynomial
References
Swamy, M. N. S. ``Further Properties of Morgan-Voyce Polynomials.'' Fib. Quart. 6, 167-175, 1968.
|
|
|
© 1996-9 Eric W. Weisstein