|
|
|
A Triangle of numbers arranged in staggered rows such that
| (1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (2) |
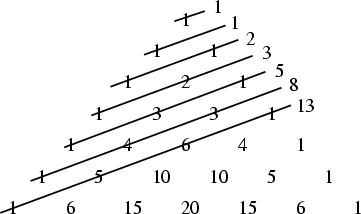
In addition, the ``Shallow Diagonals'' of Pascal's triangle sum to Fibonacci Numbers,
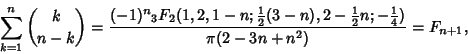 |
(3) |
where
![]() is a Generalized Hypergeometric Function.
is a Generalized Hypergeometric Function.
Pascal's triangle contains the Figurate Numbers along its diagonals. It can be shown that
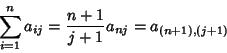 |
(4) |
| (5) |
| (6) |
 |
(7) |
It is also true that the first number after the 1 in each row divides all other numbers in that row Iff it is a
Prime. If ![]() is the number of Odd terms in the first
is the number of Odd terms in the first ![]() rows of the Pascal triangle, then
rows of the Pascal triangle, then
| (8) |
The Binomial Coefficient ![]() mod 2 can be computed using the XOR operation
mod 2 can be computed using the XOR operation ![]() XOR
XOR ![]() , making
Pascal's triangle mod 2 very easy to construct. Pascal's triangle is unexpectedly connected with the construction of
regular Polygons and with the Sierpinski Sieve.
, making
Pascal's triangle mod 2 very easy to construct. Pascal's triangle is unexpectedly connected with the construction of
regular Polygons and with the Sierpinski Sieve.
See also Bell Triangle, Binomial Coefficient, Binomial Theorem, Brianchon's Theorem, Catalan's Triangle, Clark's Triangle, Euler's Triangle, Fibonacci Number, Figurate Number Triangle, Leibniz Harmonic Triangle, Number Triangle, Pascal's Formula, Polygon, Seidel-Entringer-Arnold Triangle, Sierpinski Sieve, Trinomial Triangle
References
Conway, J. H. and Guy, R. K. ``Pascal's Triangle.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 68-70, 1996.
Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, p. 17, 1996.
Harborth, H. ``Number of Odd Binomial Coefficients.'' Not. Amer. Math. Soc. 23, 4, 1976.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 31, 1983.
Pappas, T. ``Pascal's Triangle, the Fibonacci Sequence & Binomial Formula,'' ``Chinese Triangle,'' and ``Probability and Pascal's
Triangle.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 40-41 88, and 184-186, 1989.
Sloane, N. J. A. Sequence
A007318/M0082
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Smith, D. E. A Source Book in Mathematics. New York: Dover, p. 86, 1984.
|
|
|
© 1996-9 Eric W. Weisstein