|
|
|
A triangle of numbers with entries given by
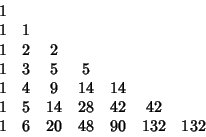
See also Bell Triangle, Clark's Triangle, Euler's Triangle, Leibniz Harmonic Triangle, Number Triangle, Pascal's Triangle, Prime Triangle, Seidel-Entringer-Arnold Triangle
References
Sloane, N. J. A. Sequence
A009766
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.