|
|
|
An Algorithm for finding the Greatest Common Divisor of two numbers ![]() and
and ![]() , also called Euclid's
algorithm. It is an example of a P-Problem whose time complexity is bounded by a quadratic function of the
length of the input values (Banach and Shallit). Let
, also called Euclid's
algorithm. It is an example of a P-Problem whose time complexity is bounded by a quadratic function of the
length of the input values (Banach and Shallit). Let ![]() , then find a number
, then find a number ![]() which Divides
both
which Divides
both ![]() and
and ![]() (so that
(so that ![]() and
and ![]() ), then
), then ![]() also Divides
also Divides ![]() since
since
| (1) |
| (2) |
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) |
| (8) |
| (9) |
| Quotient | |
| 1 | 41.5 |
| 2 | 17.0 |
| 3 | 9.3 |
For details, see Uspensky and Heaslet (1939) or Knuth (1973). Let ![]() be the number of divisions required to
compute
be the number of divisions required to
compute
![]() using the Euclidean algorithm, and define
using the Euclidean algorithm, and define ![]() if
if ![]() . Then
. Then
| (10) |
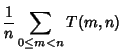 |
(11) | ||
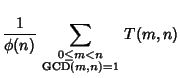 |
(12) | ||
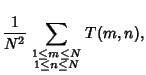 |
(13) |
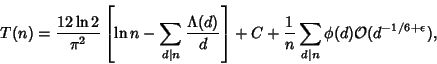 |
(14) |
| (15) |
| (16) |
There exist 22 Quadratic Fields in which there is a Euclidean algorithm (Inkeri 1947).
See also Ferguson-Forcade Algorithm
References
Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, 1996.
Courant, R. and Robbins, H. ``The Euclidean Algorithm.'' §2.4 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 42-51, 1996.
Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 69-70, 1990.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/porter/porter.html
Inkeri, K. ``Über den Euklidischen Algorithmus in quadratischen Zahlkörpern.''
Ann. Acad. Sci. Fennicae. Ser. A. I. Math.-Phys. 1947, 1-35, 1947.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1973.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1981.
Norton, G. H. ``On the Asymptotic Analysis of the Euclidean Algorithm.'' J. Symb. Comput. 10, 53-58, 1990.
Porter, J. W. ``On a Theorem of Heilbronn.'' Mathematika 22, 20-28, 1975.
Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, 1939.
Wagon, S. ``The Ancient and Modern Euclidean Algorithm'' and ``The Extended Euclidean Algorithm.'' §8.1 and 8.2
in Mathematica in Action. New York: W. H. Freeman, pp. 247-252 and 252-256, 1991.
|
|
|
© 1996-9 Eric W. Weisstein