|
|
|
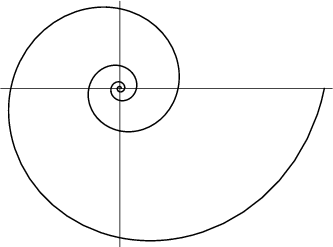
A curve whose equation in Polar Coordinates is given by
| (1) |
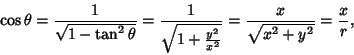 |
(2) |
| (3) | |||
| (4) |
The logarithmic spiral was first studied by Descartes ![]() in 1638 and
Jakob Bernoulli.
in 1638 and
Jakob Bernoulli. ![]() Bernoulli was so fascinated by the spiral that he had one engraved on his tombstone (although
the engraver did not draw it true to form). Torricelli worked on it independently and found the length of the curve
(MacTutor Archive).
Bernoulli was so fascinated by the spiral that he had one engraved on his tombstone (although
the engraver did not draw it true to form). Torricelli worked on it independently and found the length of the curve
(MacTutor Archive).
The rate of change of Radius is
| (5) |
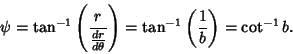 |
(6) |
If ![]() is any point on the spiral, then the length of the spiral from
is any point on the spiral, then the length of the spiral from ![]() to the origin is finite. In fact, from the point
to the origin is finite. In fact, from the point ![]() which is at distance
which is at distance ![]() from the origin measured along a Radius vector, the distance from
from the origin measured along a Radius vector, the distance from ![]() to the Pole along
the spiral is just the Arc Length. In addition, any Radius from the origin meets the spiral at distances which are
in Geometric Progression (MacTutor Archive).
to the Pole along
the spiral is just the Arc Length. In addition, any Radius from the origin meets the spiral at distances which are
in Geometric Progression (MacTutor Archive).

The Arc Length, Curvature, and Tangential Angle of the logarithmic spiral are
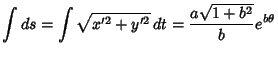 |
|||
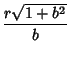 |
(7) | ||
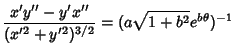 |
(8) | ||
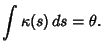 |
(9) |
| (10) |
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 184-186, 1972.
Lee, X. ``EquiangularSpiral.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/EquiangularSpiral_dir/equiangularSpiral.html
Lockwood, E. H. ``The Equiangular Spiral.'' Ch. 11 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 98-109, 1967.
MacTutor History of Mathematics Archive. ``Equiangular Spiral.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Equiangular.html.
|
|
|
© 1996-9 Eric W. Weisstein