Midpoint

The point on a Line Segment dividing it into two segments of equal length. The midpoint of a line segment is easy to locate by first constructing a Lens using circular arcs, then connecting the cusps of the Lens. The point where the cusp-connecting line intersects the segment is then the midpoint (Pedoe 1995, p. xii). It is more challenging to locate the midpoint using only a Compass, but Pedoe (1995, pp. xviii-xix) gives one solution.

In a Right Triangle, the midpoint of the Hypotenuse is equidistant from the three Vertices (Dunham 1990).

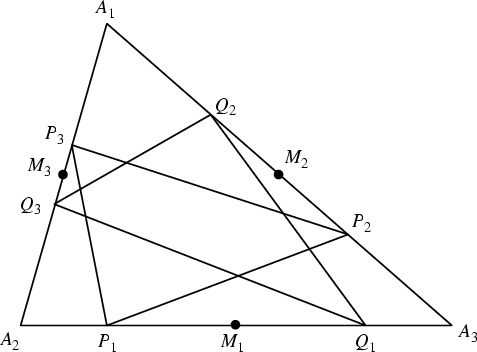
Given a Triangle $\Delta A_1A_2A_3$ with Area $\Delta$, locate the midpoints $M_i$. Now inscribe two triangles $\Delta P_1P_2P_3$ and $\Delta Q_1Q_2Q_3$ with Vertices $P_i$ and $Q_i$ placed so that $\overline{P_iM_i}= \overline{Q_iM_i}$. Then $\Delta P_1P_2P_3$ and $\Delta Q_1Q_2Q_3$ have equal areas

$$\Delta_P=\Delta_Q=\Delta \left[{1-\left({{m_1\over a_1}+{m_2... ...ver a_2a_3}+{m_3m_1\over a_3a_1}+{m_1m_2\over a_1a_2}}\right],$$

where $a_i$ are the sides of the original triangle and $m_i$ are the lengths of the Medians (Johnson 1929).

See also Archimedes' Midpoint Theorem, Brocard Midpoint, Circle-Point Midpoint Theorem, Line Segment, Median (Triangle), Midpoint Ellipse

References

Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 120-121, 1990.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, p. 80, 1929.

Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., 1995.