|
|
|
The base of the Natural Logarithm, named in honor of Euler. ![]() It appears in many mathematical contexts
involving Limits and Derivatives, and can be defined by
It appears in many mathematical contexts
involving Limits and Derivatives, and can be defined by
| (1) |
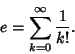 |
(2) |
| (3) |
Euler ![]() proved that
proved that ![]() is Irrational, and Liouville
is Irrational, and Liouville ![]() proved in 1844 that
proved in 1844 that ![]() does not satisfy any Quadratic Equation with integral Coefficients. Hermite
does not satisfy any Quadratic Equation with integral Coefficients. Hermite ![]() proved
proved ![]() to be Transcendental in 1873. It is not known if
to be Transcendental in 1873. It is not known if ![]() or
or ![]() is
Irrational. However, it is known that
is
Irrational. However, it is known that ![]() and
and ![]() do not satisfy any Polynomial
equation of degree
do not satisfy any Polynomial
equation of degree ![]() with Integer Coefficients of average size
with Integer Coefficients of average size ![]() (Bailey 1988,
Borwein et al. 1989).
(Bailey 1988,
Borwein et al. 1989).
The special case of the Euler Formula
| (4) |
| (5) |
Some Continued Fraction representations of ![]() include
include
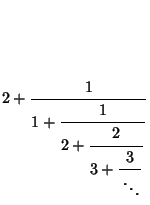 |
(6) | ||
| (7) |
| (8) | |||
| (9) | |||
| (10) | |||
| (11) |
Using the Recurrence Relation
| (12) |
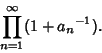 |
(13) |
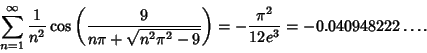 |
(14) |
Rabinowitz and Wagon (1995) give an Algorithm for computing digits of ![]() based on earlier Digits, but
a much simpler Spigot Algorithm was found by Sales (1968). Around 1966, MIT hacker Eric Jensen wrote a very concise
program (requiring less than a page of assembly language) that computed
based on earlier Digits, but
a much simpler Spigot Algorithm was found by Sales (1968). Around 1966, MIT hacker Eric Jensen wrote a very concise
program (requiring less than a page of assembly language) that computed ![]() by converting from factorial base to decimal.
by converting from factorial base to decimal.
Let ![]() be the probability that a random One-to-One function on the Integers 1, ...,
be the probability that a random One-to-One function on the Integers 1, ..., ![]() has at
least one Fixed Point. Then
has at
least one Fixed Point. Then
 |
(15) |
| (16) |
Castellanos (1988) gives several curious approximations to ![]() ,
,
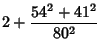 |
(17) | ||
| (18) | |||
| (19) | |||
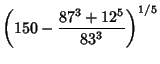 |
(20) | ||
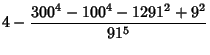 |
(21) | ||
 |
(22) |
Examples of ![]() Mnemonics (Gardner 1959, 1991) include:
Mnemonics (Gardner 1959, 1991) include:
A much more extensive mnemonic giving 40 digits is
Scanning the decimal expansion of ![]() until all
until all ![]() -digit numbers have occurred, the last appearing is 6, 12, 548, 1769, 92994, 513311,
... (Sloane's A032511). These end at positions 21, 372, 8092, 102128, 1061613, 12108841, ....
-digit numbers have occurred, the last appearing is 6, 12, 548, 1769, 92994, 513311,
... (Sloane's A032511). These end at positions 21, 372, 8092, 102128, 1061613, 12108841, ....
See also Carleman's Inequality, Compound Interest, de Moivre's Identity, Euler Formula, Exponential Function, Hermite-Lindemann Theorem, Natural Logarithm
References
Bailey, D. H. ``Numerical Results on the Transcendence of Constants Involving
Barel, Z. ``A Mnemonic for
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. ``Ramanujan, Modular Equations, and Approximations to Pi or How to
Compute One Billion Digits of Pi.'' Amer. Math. Monthly 96, 201-219, 1989.
Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 201 and 250-254, 1996.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/e/e.html
Gardner, M. ``Memorizing Numbers.'' Ch. 11 in
The Scientific American Book of Mathematical Puzzles and Diversions. New York: Simon and Schuster, pp. 103 and 109, 1959.
Gardner, M. Ch. 3 in The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago University Press,
p. 40, 1991.
Hatzipolakis, A. P. ``PiPhilology.''
http://users.hol.gr/~xpolakis/piphil.html.
Hermite, C. ``Sur la fonction exponentielle.'' C. R. Acad. Sci. Paris 77, 18-24, 74-79, and
226-233, 1873.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 47, 1983.
Maor, E. e: The Story of a Number. Princeton, NJ: Princeton University Press, 1994.
Minkus, J. ``A Continued Fraction.'' Problem 10327. Amer. Math. Monthly 103, 605-606, 1996.
Mitchell, U. G. and Strain, M. ``The Number
Olds, C. D. ``The Simple Continued Fraction Expression of
Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computation
of Constants.'' http://www.lacim.uqam.ca/pi/records.html.
Rabinowitz, S. and Wagon, S. ``A Spigot Algorithm for the Digits of
Sales, A. H. J. ``The Calculation of
Sloane, N. J. A. Sequences
A032511,
A001113/M1727,
A003417/M0088,
A007676/M0869,
A007677/M2343
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() e
e
![]() ,
, ![]() , and Euler's Constant.''
Math. Comput. 50, 275-281, 1988.
, and Euler's Constant.''
Math. Comput. 50, 275-281, 1988.
![]() .'' Math. Mag. 68, 253, 1995.
.'' Math. Mag. 68, 253, 1995.
![]() .'' Osiris 1, 476-496, 1936.
.'' Osiris 1, 476-496, 1936.
![]() .'' Amer. Math. Monthly 77, 968-974, 1970.
.'' Amer. Math. Monthly 77, 968-974, 1970.
![]() .'' Amer. Math. Monthly 102, 195-203, 1995.
.'' Amer. Math. Monthly 102, 195-203, 1995.
![]() to Many Significant Digits.'' Computer J. 11, 229-230, 1968.
to Many Significant Digits.'' Computer J. 11, 229-230, 1968.
|
|
|
© 1996-9 Eric W. Weisstein