|
|
|
Let
![]() be a Set of Positive numbers. Then the Geometric Mean and Arithmetic
Mean satisfy
be a Set of Positive numbers. Then the Geometric Mean and Arithmetic
Mean satisfy
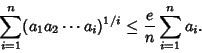
See also Arithmetic Mean, e, Geometric Mean
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1094, 1979.
Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 249-250, 1988.