|
|
|
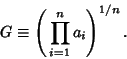
See also Arithmetic Mean, Arithmetic-Geometric Mean, Carleman's Inequality, Harmonic Mean, Mean, Root-Mean-Square
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 10, 1972.
Hoehn, L. and Niven, I. ``Averages on the Move.'' Math. Mag. 58, 151-156, 1985.