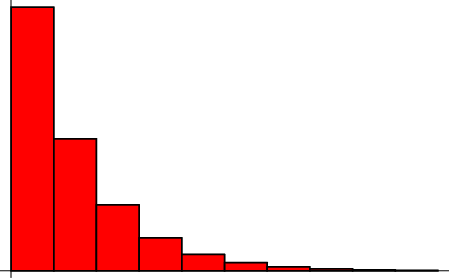
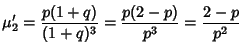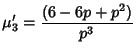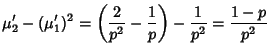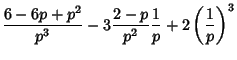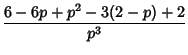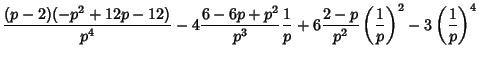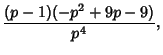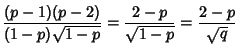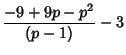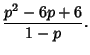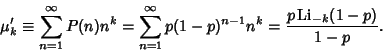A distribution such that
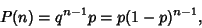 |
(1) |
where 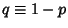 and for
and for  2, .... The distribution is normalized since
2, .... The distribution is normalized since
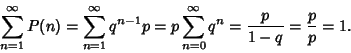 |
(2) |
The Moment-Generating Function is
![\begin{displaymath}
\phi(t)=p[1-(1-p)e^{it}]^{-1},
\end{displaymath}](g_1341.gif) |
(3) |
or
Therefore,
and
so the Mean, Variance, Skewness, and Kurtosis are given by
In fact, the moments of the distribution are given analytically in terms of the Polylogarithm function,
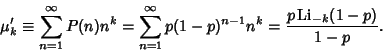 |
(19) |
For the case  (corresponding to the distribution of the number of Coin Tosses needed to win
in the Saint Petersburg Paradox) this formula immediately gives
(corresponding to the distribution of the number of Coin Tosses needed to win
in the Saint Petersburg Paradox) this formula immediately gives
so the Mean, Variance, Skewness, and Kurtosis in this case are
The first Cumulant of the geometric distribution is
 |
(28) |
and subsequent Cumulants are given by the Recurrence Relation
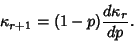 |
(29) |
See also Saint Petersburg Paradox
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 531-532,
1987.
Spiegel, M. R. Theory and Problems of Probability and Statistics.
New York: McGraw-Hill, p. 118, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
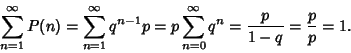
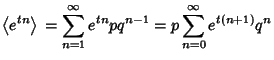

![$\displaystyle p\left[{(1-e^tq)e^t-e^t(-e^tq)\over (1-e^tq)^2}\right]$](g_1344.gif)
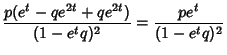

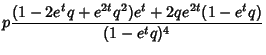
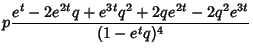
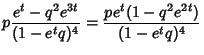

![$\displaystyle {pe^t[1+4e^t(1-p)+e^{2t}(1-p)^2]\over (1-e^t+e^tp)^4}.$](g_1352.gif)