|
|
|
Approximants derived by expanding a function as a ratio of two Power Series and determining both the Numerator and Denominator Coefficients. Padé approximations are usually superior to Taylor Expansions when functions contain Poles, because the use of Rational Functions allows them to be well-represented.
The Padé approximant ![]() corresponds to the Maclaurin Series. When it exists, the
corresponds to the Maclaurin Series. When it exists, the
![]() Padé
approximant to any Power Series
Padé
approximant to any Power Series
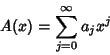 |
(1) |
| (2) |
| (3) |
| (4) |
| (5) | |||
| (6) |
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
![\begin{displaymath}[L/M]={\left\vert\matrix{
a_{L-m+1} & a_{L-m+2} & \cdots & a...
...dots & a_{L+M}\cr
x^M & x^{M-1} & \cdots & 1\cr}\right\vert},
\end{displaymath}](p1_119.gif) |
(13) |
where sums are replaced by a zero if the lower index exceeds the upper. Alternate forms are
|
|
|
|
|
![$\displaystyle \left[\begin{array}{ccc} a_{L-M+1}-xa_{L-M+2} & \cdots & a_L-xa_{...
...\ddots & \vdots\\ a_L-xa_{L+1} & \cdots & a_{L+M-1}-xa_{L+M}\end{array}\right]$](p1_123.gif) |
(14) | ||
![$\displaystyle \left[\begin{array}{c}a_{L-M+1}\\ a_{L-M+2}\\ \vdots\\ a_L\end{array}\right],$](p1_125.gif) |
(15) |
The first few Padé approximants for ![]() are
are
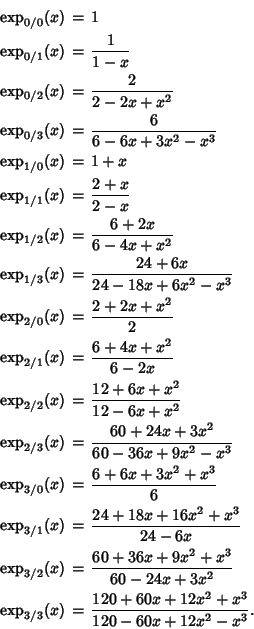
Two-term identities include
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
where ![]() is the C-Determinant. Three-term identities can be derived using the
Frobenius Triangle Identities (Baker 1975, p. 32).
is the C-Determinant. Three-term identities can be derived using the
Frobenius Triangle Identities (Baker 1975, p. 32).
A five-term identity is
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
See also C-Determinant, Economized Rational Approximation, Frobenius Triangle Identities
References
Baker, G. A. Jr. ``The Theory and Application of The Pade Approximant Method.'' In Advances in Theoretical Physics, Vol. 1
(Ed. K. A. Brueckner). New York: Academic Press, pp. 1-58, 1965.
Baker, G. A. Jr. Essentials of Padé Approximants in Theoretical Physics. New York: Academic Press, pp. 27-38, 1975.
Baker, G. A. Jr. and Graves-Morris, P. Padé Approximants. New York: Cambridge University Press, 1996.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Padé Approximants.'' §5.12 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 194-197, 1992.
![]() Padé Approximants
Padé Approximants
|
|
|
© 1996-9 Eric W. Weisstein