|
|
|
A Taylor series is a series expansion of a Function about a point. A 1-D Taylor series is an expansion of a
Scalar Function ![]() about a point
about a point ![]() . If
. If ![]() , the expansion is known as a Maclaurin Series.
, the expansion is known as a Maclaurin Series.
| (1) |
|
|
|
|
|
(2) |
| (3) |

|
|
|
|
(4) |
|
|
|
|
|
(5) |
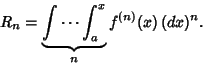 |
(6) |
| (7) |
| (8) |
An alternative form of the 1-D Taylor series may be obtained by letting
| (9) |
| (10) |
| (11) |
A Taylor series of a Function in two variables ![]() is given by
is given by
|
|
|
|
|
|
|
|
|
|
|
(12) |
This can be further generalized for a Function in ![]() variables,
variables,
 |
(13) |
Rewriting,
|
|
|
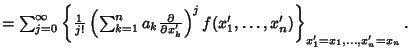
|
|
|
|
(14) |
Taking ![]() in (13) gives
in (13) gives
![$f(x_1,x_2)=\sum_{j=0}^\infty \left\{{{1\over j!}\left[{(x_1'-a_1){\partial \ove...
...artial \over \partial x_2'}}\right]^j f(x_1',x_2')}\right\}_{x_1'=x_1,x_2'=x_2}$](t_290.gif)
|
|
|
|
|
|
|
(15) |
Taking ![]() in (14) gives
in (14) gives
|
|
|
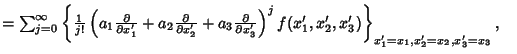
|
(16) |
![\begin{displaymath}
f({\bf r}+{\bf a}) = \sum_{j=0}^\infty \left[{\,{1\over j!} ...
...ot\nabla_{{\bf r}'})^j f({\bf r}')}\right]_{{\bf r}'={\bf r}}.
\end{displaymath}](t_296.gif) |
(17) |
| (18) |
| (19) |
| (20) |
| (21) |
Taylor series can also be defined for functions of a Complex variable. By the Cauchy Integral Formula,
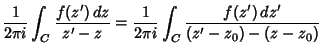 |
|||
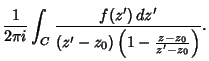 |
(22) |
| (23) |
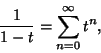 |
(24) |
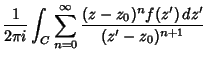 |
|||
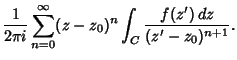 |
(25) |
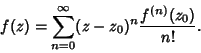 |
(26) |
See also Cauchy Remainder Form, Lagrange Expansion, Laurent Series, Legendre Series, Maclaurin Series, Newton's Forward Difference Formula
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 880, 1972.
Arfken, G. ``Taylor's Expansion.'' §5.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 303-313, 1985.
Morse, P. M. and Feshbach, H. ``Derivatives of Analytic Functions, Taylor and Laurent Series.'' §4.3 in
Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 374-398, 1953.
|
|
|
© 1996-9 Eric W. Weisstein