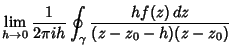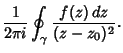Given a Contour Integral of the form
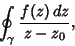 |
(1) |
define a path 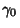 as an infinitesimal Circle around the point
as an infinitesimal Circle around the point 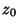 (the dot in the above illustration).
Define the path
(the dot in the above illustration).
Define the path 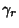 as an arbitrary loop with a cut line (on which the forward and reverse contributions cancel
each other out) so as to go around
as an arbitrary loop with a cut line (on which the forward and reverse contributions cancel
each other out) so as to go around 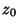 .
.
The total path is then
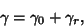 |
(2) |
so
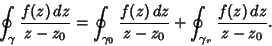 |
(3) |
From the Cauchy Integral Theorem, the Contour Integral along any path not enclosing a Pole is 0.
Therefore, the first term in the above equation is 0 since 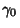 does not enclose the Pole, and we are left
with
does not enclose the Pole, and we are left
with
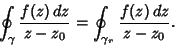 |
(4) |
Now, let
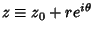 , so
, so
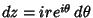 . Then
. Then
But we are free to allow the radius 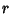 to shrink to 0, so
to shrink to 0, so
and
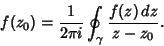 |
(7) |
If multiple loops are made around the Pole, then equation (7) becomes
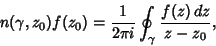 |
(8) |
where 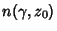 is the Winding Number.
is the Winding Number.
A similar formula holds for the derivatives of 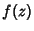 ,
,
Iterating again,
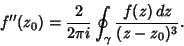 |
(10) |
Continuing the process and adding the Winding Number 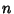 ,
,
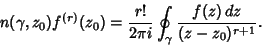 |
(11) |
See also Morera's Theorem
References
Arfken, G. ``Cauchy's Integral Formula.'' §6.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 371-376, 1985.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 367-372, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26
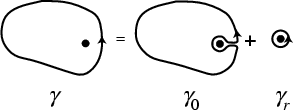
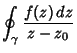
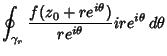
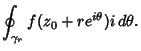
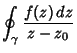
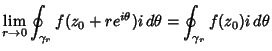
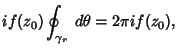
![]() ,
,
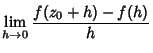
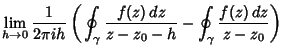
![$\displaystyle \lim_{h\to 0} {1\over 2\pi ih} \oint_\gamma {f(z)[(z-z_0)-(z-z_0-h)]\,dz\over (z-z_0-h)(z-z_0)}$](c1_671.gif)