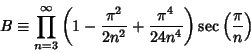If a Triangle is Circumscribed about a Circle, another Circle around the Triangle, a
Square outside the Circle, another Circle outside the Square, and so on. From
Polygons, the Circumradius and Inradius for an 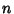 -gon are
-gon are
where 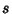 is the side length. Therefore,
is the side length. Therefore,
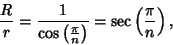 |
(3) |
and an infinitely nested set of circumscribed polygons and circles has
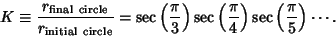 |
(4) |
Kasner and Newman (1989) and Haber (1964) state that 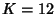 , but this is incorrect. Write
, but this is incorrect. Write
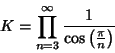 |
(5) |
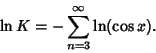 |
(6) |
Define
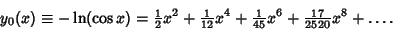 |
(7) |
Now define
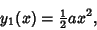 |
(8) |
with
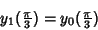 |
(9) |
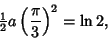 |
(10) |
so
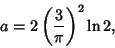 |
(11) |
and
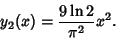 |
(12) |
But 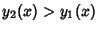 for
for
 , so
, so
![\begin{displaymath}
\sum_{n=3}^\infty y_2\left({\pi\over n}\right)> -\sum_{n=3}^\infty \ln\left[{\cos\left({\pi\over n}\right)}\right]
\end{displaymath}](p2_1342.gif) |
(13) |
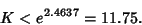 |
(15) |
If the next term is included,
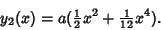 |
(16) |
As before,
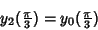 |
(17) |
 |
(18) |
so
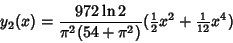 |
(19) |
and
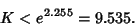 |
(21) |
The process can be automated using computer algebra, and the first few bounds are 11.7485, 9.53528, 8.98034, 8.8016,
8.73832, 8.71483, 8.70585, 8.70235, 8.70097, and 8.70042. In order to obtain this accuracy by direct multiplication
of the terms, more than 10,000 terms are needed. The limit is
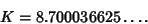 |
(22) |
Bouwkamp (1965) produced the following Infinite Product formulas
where 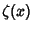 is the Riemann Zeta Function and
is the Riemann Zeta Function and  is the Dirichlet Lambda Function.
Bouwkamp (1965) also produced the formula with accelerated convergence
is the Dirichlet Lambda Function.
Bouwkamp (1965) also produced the formula with accelerated convergence
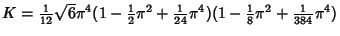
|
|

|
(25) |
where
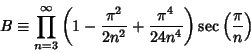 |
(26) |
(cited in Pickover 1995).
See also Polygon Inscribing Constant
References
Bouwkamp, C. ``An Infinite Product.'' Indag. Math. 27, 40-46, 1965.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/infprd/infprd.html
Haber, H. ``Das Mathematische Kabinett.'' Bild der Wissenschaft 2, 73, Apr. 1964.
Kasner, E. and Newman, J. R. Mathematics and the Imagination. Redmond, WA: Microsoft Press, pp. 311-312, 1989.
Pappas, T. ``Infinity & Limits.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, p. 180, 1989.
Pickover, C. A. ``Infinitely Exploding Circles.'' Ch. 18 in Keys to Infinity.
New York: W. H. Freeman, pp. 147-151, 1995.
Pinkham, R. S. ``Mathematics and Modern Technology.'' Amer. Math. Monthly 103, 539-545, 1996.
Plouffe, S. ``Product(cos(Pi/n),n=3..infinity).''
http://www.lacim.uqam.ca/piDATA/productcos.txt.
© 1996-9 Eric W. Weisstein
1999-05-25
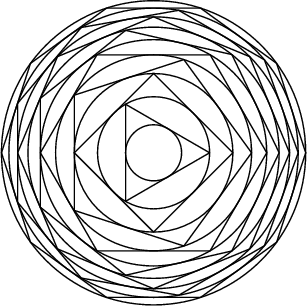
![]() -gon are
-gon are
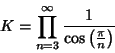
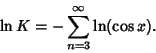
![\begin{displaymath}
\sum_{n=3}^\infty y_2\left({\pi\over n}\right)> -\sum_{n=3}^\infty \ln\left[{\cos\left({\pi\over n}\right)}\right]
\end{displaymath}](p2_1342.gif)
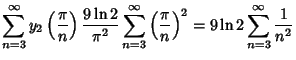
![$\displaystyle 9\ln 2\left({\sum_{n=1}^\infty {1\over n^2}-\sum_{n=1}^2 {1\over n^2}}\right)= 9\ln 2[\zeta(2)-{\textstyle{5\over 4}}]$](p2_1345.gif)
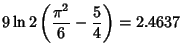
![$\displaystyle {972\ln 2\over \pi^2(54+\pi^2)} \sum_{n=3}^\infty \left[{{1\over 2}\left({\pi\over n}\right)^2 +{1\over 12}\left({\pi\over n}\right)^4}\right]$](p2_1352.gif)
![$\displaystyle {972\ln 2\over \pi^2(54+\pi^2)}\left\{{{1\over 2}\left[{\zeta(2)-{5\over 4}}\right]
+{\pi^2\over 12}\left[{\zeta(4)-1-{1\over 2^4}}\right]}\right\}$](p2_1353.gif)
![$\displaystyle {972\ln 2\over \pi^2(54+\pi^2)}\left[{{1\over 2}\left({{\pi^2\ove...
...}}\right)
+{\pi^2\over 12}\left({{\pi^4\over 90}-1-{1\over 2^4}}\right)}\right]$](p2_1354.gif)
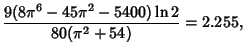
![$\displaystyle {2\over\pi}\prod_{m=1}^\infty\prod_{n=1}^\infty \left[{1-{1\over m^2(n+{\textstyle{1\over 2}})^2}}\right]$](p2_1359.gif)
![$\displaystyle 6\mathop{\rm exp}\nolimits \left\{{\sum_{k=1}^\infty {[\lambda(2k)-1]2^{2k}[\zeta(2k)-1-2^{-2k}]\over k}}\right\},$](p2_1360.gif)