|
|
|
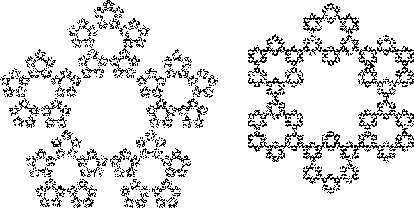
Pick a point at random inside a regular ![]() -gon. Then draw the next point a fraction
-gon. Then draw the next point a fraction ![]() of the distance between it and a
Vertex picked at random. Continue the process (after throwing out the first few points). The
result of this ``chaos game'' is sometimes, but not always, a Fractal. The case
of the distance between it and a
Vertex picked at random. Continue the process (after throwing out the first few points). The
result of this ``chaos game'' is sometimes, but not always, a Fractal. The case ![]() gives the
interior of a Square with all points visited with equal probability.
gives the
interior of a Square with all points visited with equal probability.

![]()
![]()
![]()
![]()
See also Barnsley's Fern
References
Barnsley, M. F. and Rising, H. Fractals Everywhere, 2nd ed. Boston, MA: Academic Press, 1993.
Dickau, R. M. ``The Chaos Game.''
http://forum.swarthmore.edu/advanced/robertd/chaos_game.html.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 149-163, 1991.
![]() Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.
Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.