Trisection

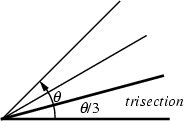
$\begin{figure}\begin{center}\BoxedEPSF{TrisectionAngle.epsf scaled 800}\end{center}\end{figure}$

Angle trisection is the division of an arbitrary Angle into three equal Angles. It was one of the three Geometric Problems of Antiquity for which solutions using only Compass and Straightedge were sought. The problem was algebraically proved impossible by Wantzel (1836).

Although trisection is not possible for a general Angle using a Greek construction, there are some specific angles, such as $\pi/2$ and $\pi$ radians (90° and 180°, respectively), which can be trisected. Furthermore, some Angles are geometrically trisectable, but cannot be constructed in the first place, such as $3\pi/7$ (Honsberger 1991). In addition, trisection of an arbitrary angle can be accomplished using a marked Ruler (a Neusis Construction) as illustrated below (Courant and Robbins 1996).

$\begin{figure}\begin{center}\BoxedEPSF{Trisection.epsf scaled 900}\end{center}\end{figure}$

An Angle can also be divided into three (or any Whole Number) of equal parts using the Quadratrix of Hippias or Trisectrix.

References

Bogomolny, A. ``Angle Trisection.'' http://www.cut-the-knot.com/pythagoras/archi.html.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 190-191, 1996.

Courant, R. and Robbins, H. ``Trisecting the Angle.'' §3.3.3 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 137-138, 1996.

Coxeter, H. S.M. ``Angle Trisection.'' §2.2 in Introduction to Geometry, 2nd ed. New York: Wiley, p. 28, 1969.

Dixon, R. Mathographics. New York: Dover, pp. 50-51, 1991.

Dörrie, H. ``Trisection of an Angle.'' §36 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 172-177, 1965.

Dudley, U. The Trisectors. Washington, DC: Math. Assoc. Amer., 1994.

Geometry Center. ``Angle Trisection.'' http://www.geom.umn.edu:80/docs/forum/angtri/.

Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 25-26, 1991.

Ogilvy, C. S. ``Angle Trisection.'' Excursions in Geometry. New York: Dover, pp. 135-141, 1990.

Wantzel, M. L. ``Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas.'' J. Math. pures appliq. 1, 366-372, 1836.